Bài Tập Về Kỳ Vọng Có Lời Giải là một chủ đề quan trọng trong toán học, đặc biệt là trong xác suất thống kê. Việc nắm vững kiến thức và kỹ năng giải bài tập về kỳ vọng sẽ giúp học sinh, sinh viên áp dụng vào nhiều lĩnh vực khác nhau. Bài viết này cung cấp hướng dẫn chi tiết về cách giải bài tập về kỳ vọng, từ cơ bản đến nâng cao, kèm theo lời giải và ví dụ minh họa.
Khái Niệm Kỳ Vọng Và Ứng Dụng
Kỳ vọng (hay giá trị trung bình) của một biến ngẫu nhiên là giá trị trung bình của biến đó khi thực hiện một số lượng lớn các phép thử. Nó thể hiện xu hướng trung tâm của phân phối xác suất. Kỳ vọng được ứng dụng rộng rãi trong nhiều lĩnh vực, từ kinh tế, tài chính đến vật lý, kỹ thuật. Ví dụ, trong tài chính, kỳ vọng được sử dụng để tính toán lợi nhuận trung bình của một khoản đầu tư. Trong vật lý, kỳ vọng được sử dụng để tính toán vị trí trung bình của một hạt.
Các Dạng Bài Tập Về Kỳ Vọng Thường Gặp
Bài tập về kỳ vọng có nhiều dạng khác nhau, từ đơn giản đến phức tạp. Dưới đây là một số dạng bài tập thường gặp:
- Bài tập tính kỳ vọng của biến ngẫu nhiên rời rạc: Đây là dạng bài tập cơ bản, yêu cầu tính kỳ vọng của một biến ngẫu nhiên có thể nhận một số hữu hạn hoặc vô hạn đếm được các giá trị.
- Bài tập tính kỳ vọng của biến ngẫu nhiên liên tục: Dạng bài tập này yêu cầu tính kỳ vọng của một biến ngẫu nhiên có thể nhận bất kỳ giá trị nào trong một khoảng xác định.
- Bài tập tính kỳ vọng của hàm của biến ngẫu nhiên: Dạng bài tập này yêu cầu tính kỳ vọng của một hàm của một biến ngẫu nhiên.
- Bài tập ứng dụng kỳ vọng trong các bài toán thực tế: Dạng bài tập này yêu cầu áp dụng kiến thức về kỳ vọng để giải quyết các vấn đề thực tế trong các lĩnh vực khác nhau.
Ví Dụ Về Bài Tập Kỳ Vọng Có Lời Giải
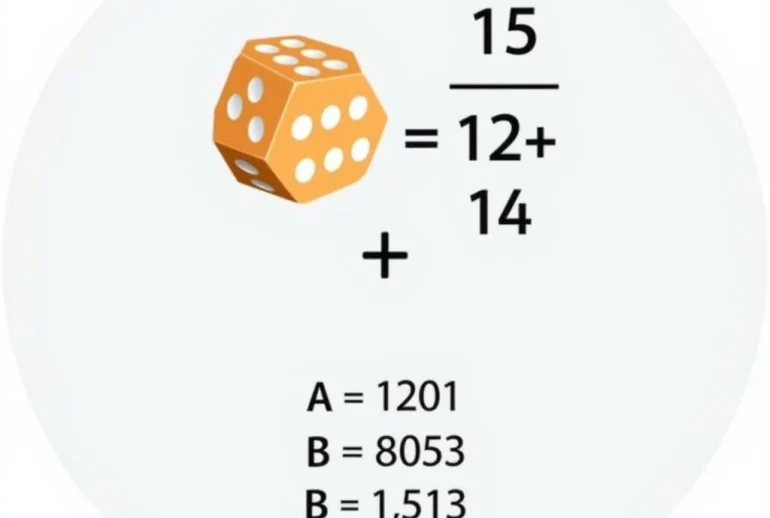
Bài toán: Một con xúc xắc được gieo một lần. Tính kỳ vọng của số chấm xuất hiện.
Lời giải: Gọi X là biến ngẫu nhiên biểu thị số chấm xuất hiện khi gieo con xúc xắc. X có thể nhận các giá trị từ 1 đến 6, mỗi giá trị có xác suất là 1/6. Kỳ vọng của X được tính như sau:
E(X) = 1(1/6) + 2(1/6) + 3(1/6) + 4(1/6) + 5(1/6) + 6(1/6) = 3.5
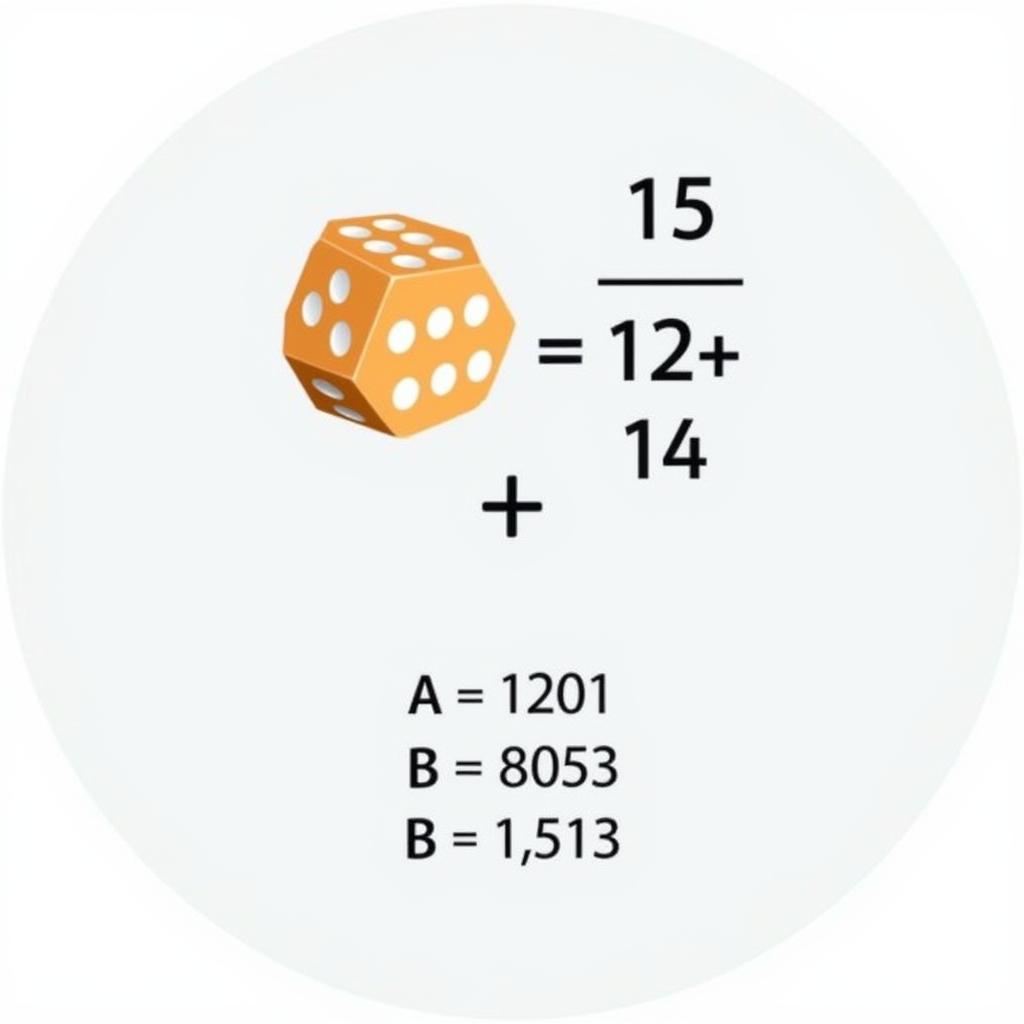Tính kỳ vọng khi gieo xúc xắc
Vậy kỳ vọng của số chấm xuất hiện khi gieo con xúc xắc là 3.5.
Mẹo Giải Bài Tập Về Kỳ Vọng
Để giải bài tập về kỳ vọng hiệu quả, học sinh, sinh viên cần nắm vững các công thức tính kỳ vọng, hiểu rõ khái niệm biến ngẫu nhiên và phân phối xác suất. Ngoài ra, việc luyện tập thường xuyên với các bài tập từ cơ bản đến nâng cao cũng rất quan trọng.
cách giải bài toán lớp 6 trang 56
Phương Pháp Học Hiệu Quả
Một phương pháp học hiệu quả là chia nhỏ các bài toán phức tạp thành các bài toán nhỏ hơn, dễ giải quyết hơn. Sau đó, kết hợp các kết quả của các bài toán nhỏ để tìm ra lời giải cho bài toán ban đầu.
giải bài tập hóa 12 bài 1 este nâng cao
Kết Luận
Bài viết này đã cung cấp những kiến thức cơ bản về bài tập về kỳ vọng có lời giải, từ khái niệm, các dạng bài tập đến mẹo giải bài tập. Hy vọng bài viết sẽ giúp ích cho học sinh, sinh viên trong quá trình học tập và nghiên cứu.
giải bài 3 trang 148 toán đại 10
FAQ
- Kỳ vọng của một biến ngẫu nhiên là gì?
- Làm thế nào để tính kỳ vọng của một biến ngẫu nhiên rời rạc?
- Làm thế nào để tính kỳ vọng của một biến ngẫu nhiên liên tục?
- Ứng dụng của kỳ vọng trong thực tế là gì?
- Làm thế nào để học hiệu quả về kỳ vọng?
- Có những tài liệu nào hỗ trợ học tập về kỳ vọng?
- bài 89 sbt toán 7 tập 1 lời giải hay Bài tập về kỳ vọng có liên quan đến những chủ đề nào khác trong toán học?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc xác định đúng loại biến ngẫu nhiên (rời rạc hay liên tục) và áp dụng công thức tính kỳ vọng tương ứng. Việc phân biệt giữa kỳ vọng và các đại lượng thống kê khác như phương sai, độ lệch chuẩn cũng là một thử thách.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về cách giải dạng bài tìm số hạng ko chứa x.
