Giải thuật di truyền là một phương pháp tối ưu mạnh mẽ, được ứng dụng rộng rãi trong nhiều lĩnh vực. Bài viết này sẽ khám phá chi tiết về Bài Tập Giải Thuật Di Truyền, từ cơ bản đến nâng cao, giúp bạn hiểu rõ hơn về cách thức hoạt động và ứng dụng của nó.
Giải Thuật Di Truyền là gì?
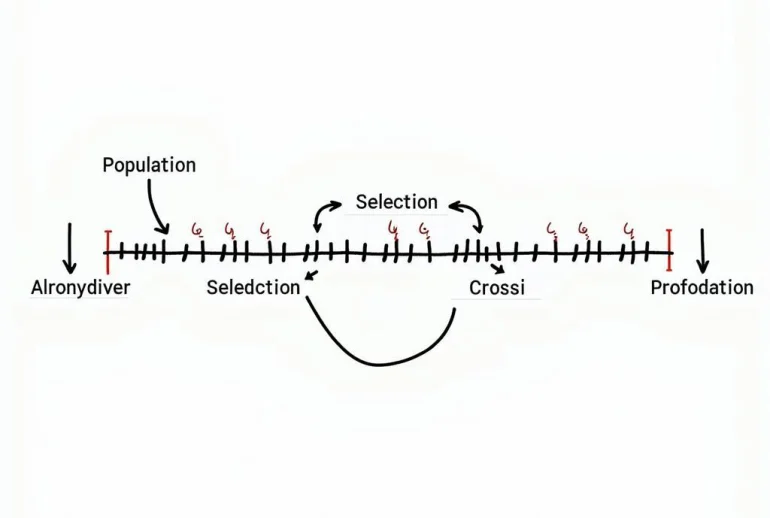
Giải thuật di truyền (GA – Genetic Algorithm) là một thuật toán tìm kiếm dựa trên cơ chế chọn lọc tự nhiên và di truyền học. GA mô phỏng quá trình tiến hóa của các sinh vật trong tự nhiên, trong đó các cá thể tốt nhất được chọn lọc để tạo ra thế hệ tiếp theo. Quá trình này lặp lại cho đến khi tìm được giải pháp tối ưu hoặc đạt đến một tiêu chí dừng nhất định.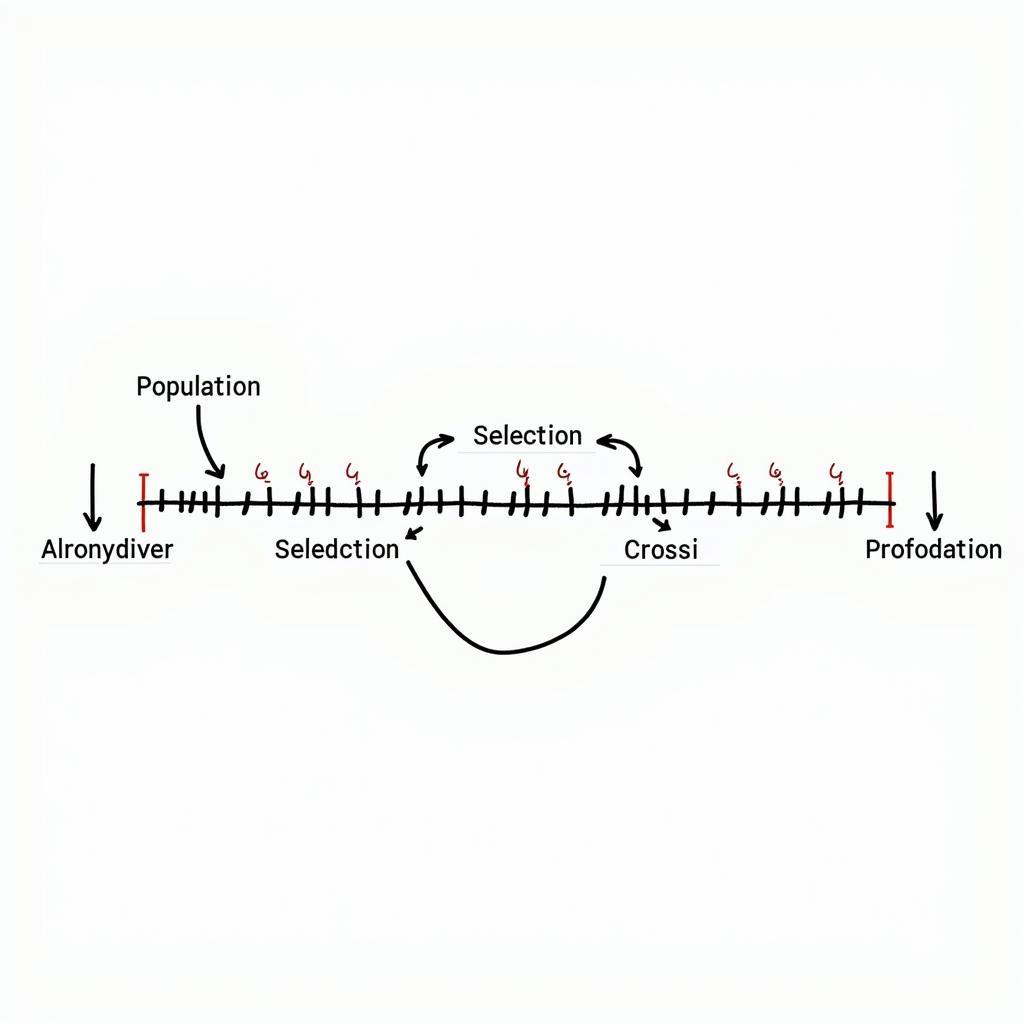 
Hình ảnh minh họa giải thuật di truyền cơ bản
bài tập và lời giải nhiệt học yung-kuo lim
Các Thành Phần Chính của Giải Thuật Di Truyền
Một giải thuật di truyền bao gồm các thành phần chính sau:
- Quần thể (Population): Tập hợp các cá thể (giải pháp tiềm năng).
- Cá thể (Individual): Một giải pháp tiềm năng cho bài toán.
- Nhiễm sắc thể (Chromosome): Biểu diễn của một cá thể, thường là một chuỗi bit hoặc số.
- Gen (Gene): Một phần tử của nhiễm sắc thể.
- Hàm thích nghi (Fitness Function): Đánh giá chất lượng của mỗi cá thể.
- Chọn lọc (Selection): Chọn các cá thể tốt nhất để tạo ra thế hệ tiếp theo.
- Lai ghép (Crossover): Kết hợp các gen của hai cá thể cha mẹ để tạo ra con cái.
- Đột biến (Mutation): Thay đổi ngẫu nhiên một hoặc nhiều gen của cá thể.
Các Bước Thực Hiện Giải Thuật Di Truyền
Để thực hiện giải thuật di truyền, ta cần thực hiện các bước sau:
- Khởi tạo quần thể: Tạo một quần thể ban đầu gồm các cá thể ngẫu nhiên.
- Đánh giá độ thích nghi: Tính toán giá trị hàm thích nghi cho mỗi cá thể.
- Chọn lọc: Chọn các cá thể có độ thích nghi cao.
- Lai ghép: Lai ghép các cá thể được chọn để tạo ra con cái.
- Đột biến: Đột biến một số gen của con cái.
- Thay thế: Thay thế các cá thể cũ bằng con cái mới.
- Lặp lại bước 2-6: Cho đến khi đạt được điều kiện dừng.
Ví Dụ Bài Tập Giải Thuật Di Truyền
Giả sử ta muốn tìm giá trị lớn nhất của hàm f(x) = x^2 trong khoảng [0, 31]. Ta có thể sử dụng giải thuật di truyền để giải bài toán này. Mỗi cá thể sẽ được biểu diễn bằng một chuỗi 5 bit (vì 2^5 = 32).
bài toán đơn hình mở rộng giải bài toán m
Ứng Dụng của Giải Thuật Di Truyền
Giải thuật di truyền được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Tối ưu hóa hàm số: Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số.
- Học máy: Huấn luyện các mô hình học máy.
- Kỹ thuật điều khiển: Điều khiển các hệ thống phức tạp.
- Sinh học tính toán: Mô phỏng các quá trình sinh học.
Giải Thuật Di Truyền trong Python
Python cung cấp nhiều thư viện hỗ trợ việc thực hiện giải thuật di truyền, chẳng hạn như DEAP.
Hình ảnh minh họa ứng dụng giải thuật di truyền trong python
Kết Luận
Bài tập giải thuật di truyền là một công cụ mạnh mẽ giúp giải quyết các bài toán tối ưu phức tạp. Việc hiểu rõ về các thành phần và bước thực hiện của giải thuật di truyền sẽ giúp bạn áp dụng nó hiệu quả trong nhiều lĩnh vực khác nhau.
FAQ
- Giải thuật di truyền có ưu điểm gì? Khả năng tìm kiếm toàn cục, dễ dàng song song hóa, và áp dụng được cho nhiều loại bài toán.
- Giải thuật di truyền có nhược điểm gì? Tốn thời gian tính toán, khó xác định các tham số tối ưu.
- Làm thế nào để chọn hàm thích nghi phù hợp? Hàm thích nghi cần phản ánh chính xác mục tiêu của bài toán.
- Khi nào nên sử dụng giải thuật di truyền? Khi bài toán có không gian tìm kiếm lớn và phức tạp.
- Có những biến thể nào của giải thuật di truyền? Có nhiều biến thể như NSGA-II, SPEA2, MOEA/D.
- Tôi có thể tìm hiểu thêm về giải thuật di truyền ở đâu? Có nhiều tài liệu trực tuyến và sách về giải thuật di truyền.
- Làm thế nào để cài đặt giải thuật di truyền trong Python? Sử dụng các thư viện như DEAP.
các bài dự thi kiến thức liên môn đạt giải
bài 3 giải pháp để tích tụ ruộng đất
Khi cần hỗ trợ hãy liên hệ Email: [email protected], địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
