Giải Bài Tập 4 Sgk Toán Hình 11 Trang 33 là một trong những bài toán quan trọng giúp học sinh nắm vững kiến thức về phép biến hình, cụ thể là phép đối xứng tâm. Bài viết này sẽ cung cấp lời giải chi tiết cho bài tập 4, kèm theo những bài tập mở rộng và phương pháp học tập hiệu quả.
Phép Đối Xứng Tâm và Bài Tập 4 SGK Toán Hình 11 Trang 33
Bài tập 4 sgk toán hình 11 trang 33 yêu cầu học sinh vận dụng kiến thức về phép đối xứng tâm để giải quyết vấn đề hình học. Phép đối xứng tâm là một phép biến hình quan trọng, có ứng dụng rộng rãi trong toán học và đời sống. Việc nắm vững kiến thức này sẽ giúp học sinh giải quyết nhiều bài toán hình học phức tạp hơn.
- Định nghĩa phép đối xứng tâm: Phép đối xứng tâm I biến điểm M thành điểm M’ sao cho I là trung điểm của đoạn thẳng MM’.
- Tính chất của phép đối xứng tâm: Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm, biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó.
Để giải bài tập 4 sgk toán hình 11 trang 33, chúng ta cần xác định tâm đối xứng và áp dụng các tính chất của phép đối xứng tâm. Đề bài thường yêu cầu tìm ảnh của một hình qua phép đối xứng tâm hoặc chứng minh hai hình đối xứng với nhau qua một tâm.
Hướng Dẫn Giải Chi Tiết Bài Tập 4 SGK Toán Hình 11 Trang 33
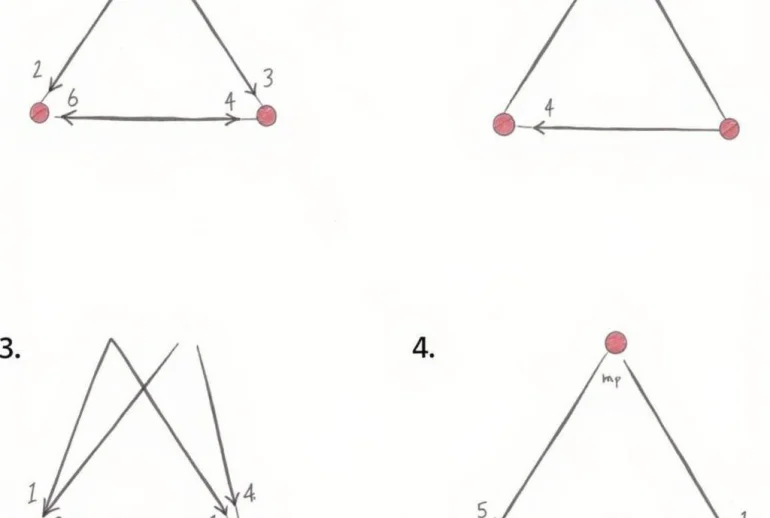
Chúng ta sẽ phân tích đề bài và đưa ra lời giải chi tiết từng bước. Giả sử đề bài yêu cầu tìm ảnh của tam giác ABC qua phép đối xứng tâm O.
- Xác định tâm đối xứng: Tâm đối xứng O đã được cho trong đề bài.
- Tìm ảnh của từng đỉnh: Tìm ảnh A’, B’, C’ của các đỉnh A, B, C qua phép đối xứng tâm O. A’, B’, C’ lần lượt là các điểm sao cho O là trung điểm của AA’, BB’, CC’.
- Kết luận: Tam giác A’B’C’ là ảnh của tam giác ABC qua phép đối xứng tâm O.
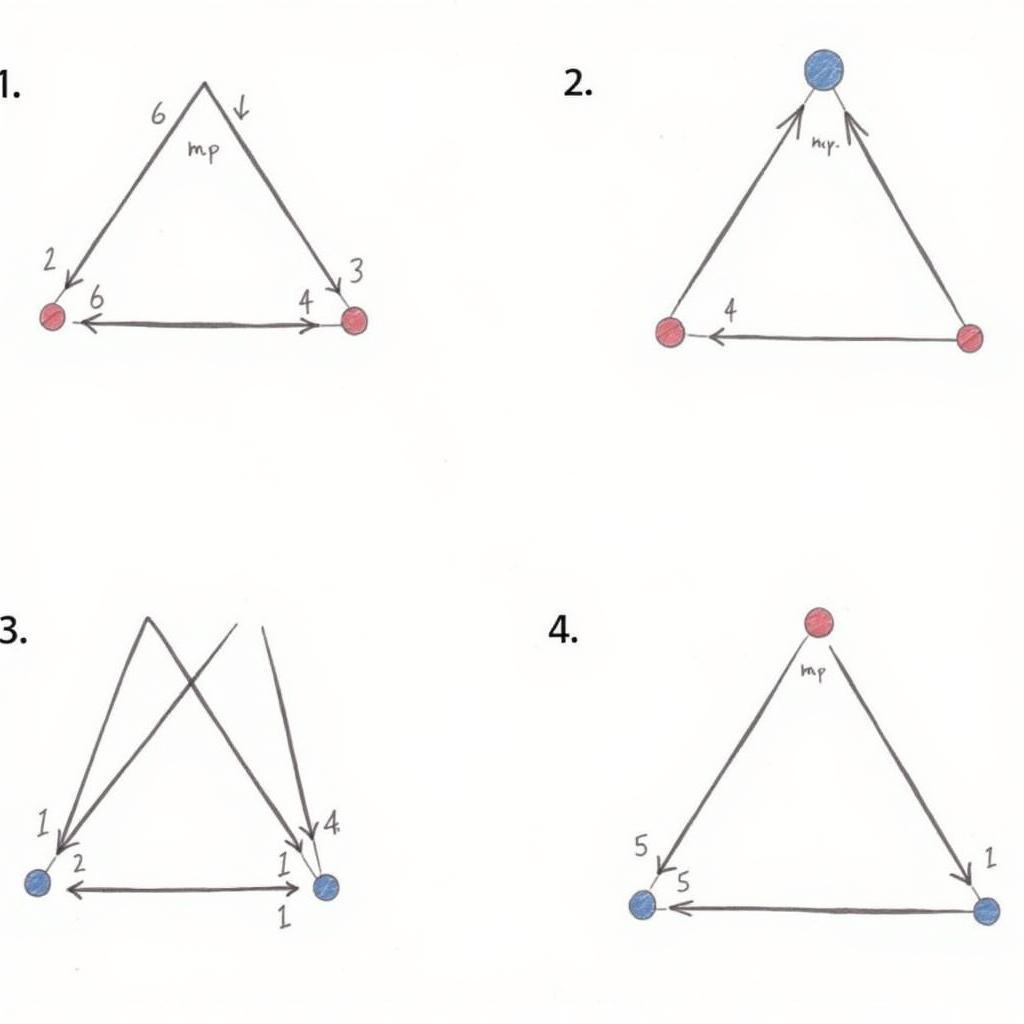Giải Bài Tập 4 Toán Hình 11 Trang 33 Hình 2
Bài Tập Mở Rộng Về Phép Đối Xứng Tâm
Để củng cố kiến thức, chúng ta sẽ cùng xem xét một số bài tập mở rộng.
- Bài tập 1: Cho hình vuông ABCD tâm O. Tìm ảnh của hình vuông ABCD qua phép đối xứng tâm O.
- Bài tập 2: Cho hai điểm A và B. Tìm tập hợp các điểm M sao cho tam giác MAB cân tại M.
Giải quyết các bài tập mở rộng này sẽ giúp học sinh nâng cao khả năng tư duy và vận dụng kiến thức về phép đối xứng tâm.
Mẹo Học Tập Hiệu Quả Với Toán Hình 11
- Vẽ hình chính xác: Vẽ hình chính xác là bước quan trọng để hiểu và giải quyết bài toán hình học.
- Nắm vững định nghĩa và tính chất: Hiểu rõ định nghĩa và tính chất của phép đối xứng tâm là điều kiện tiên quyết để giải bài tập.
- Luyện tập thường xuyên: Giải nhiều bài tập sẽ giúp học sinh thành thạo và tự tin hơn.
Kết luận
Giải bài tập 4 sgk toán hình 11 trang 33 không chỉ giúp học sinh nắm vững kiến thức về phép đối xứng tâm mà còn rèn luyện khả năng tư duy logic và giải quyết vấn đề. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích.
FAQ
- Phép đối xứng tâm là gì?
- Tính chất của phép đối xứng tâm là gì?
- Làm thế nào để tìm ảnh của một hình qua phép đối xứng tâm?
- Ứng dụng của phép đối xứng tâm trong thực tế là gì?
- Làm thế nào để học tốt toán hình 11?
- Có những phương pháp nào để giải bài tập về phép đối xứng tâm?
- Tài liệu nào hữu ích cho việc học toán hình 11?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc xác định tâm đối xứng và tìm ảnh của các hình phức tạp qua phép đối xứng tâm. Việc luyện tập thường xuyên và vẽ hình chính xác sẽ giúp khắc phục những khó khăn này.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các phép biến hình khác như phép tịnh tiến, phép quay, phép vị tự trên website BaDaoVl.
