Giải phương trình bằng phương pháp chia đôi là một phương pháp số học kinh điển, được sử dụng rộng rãi để tìm nghiệm gần đúng của phương trình. Bài viết này sẽ hướng dẫn bạn chi tiết về phương pháp chia đôi, từ nguyên lý cơ bản đến các ví dụ minh họa và ứng dụng thực tế.
Nguyên Lý Phương Pháp Chia Đôi
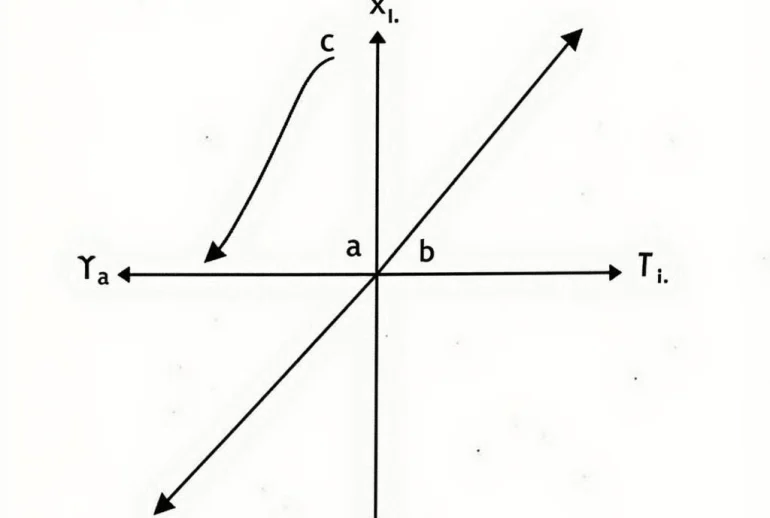
Phương pháp chia đôi dựa trên định lý Bolzano, nói rằng nếu một hàm số liên tục f(x) có giá trị trái dấu tại hai điểm a và b (tức là f(a) * f(b) < 0), thì tồn tại ít nhất một nghiệm của phương trình f(x) = 0 trong khoảng (a, b). Phương pháp này liên tục thu hẹp khoảng (a, b) bằng cách lấy trung điểm c = (a + b) / 2. Nếu f(c) = 0, thì c là nghiệm. Nếu f(c) cùng dấu với f(a), nghiệm nằm trong khoảng (c, b); ngược lại, nghiệm nằm trong khoảng (a, c). Quá trình này lặp lại cho đến khi khoảng (a, b) đủ nhỏ, đạt độ chính xác mong muốn.
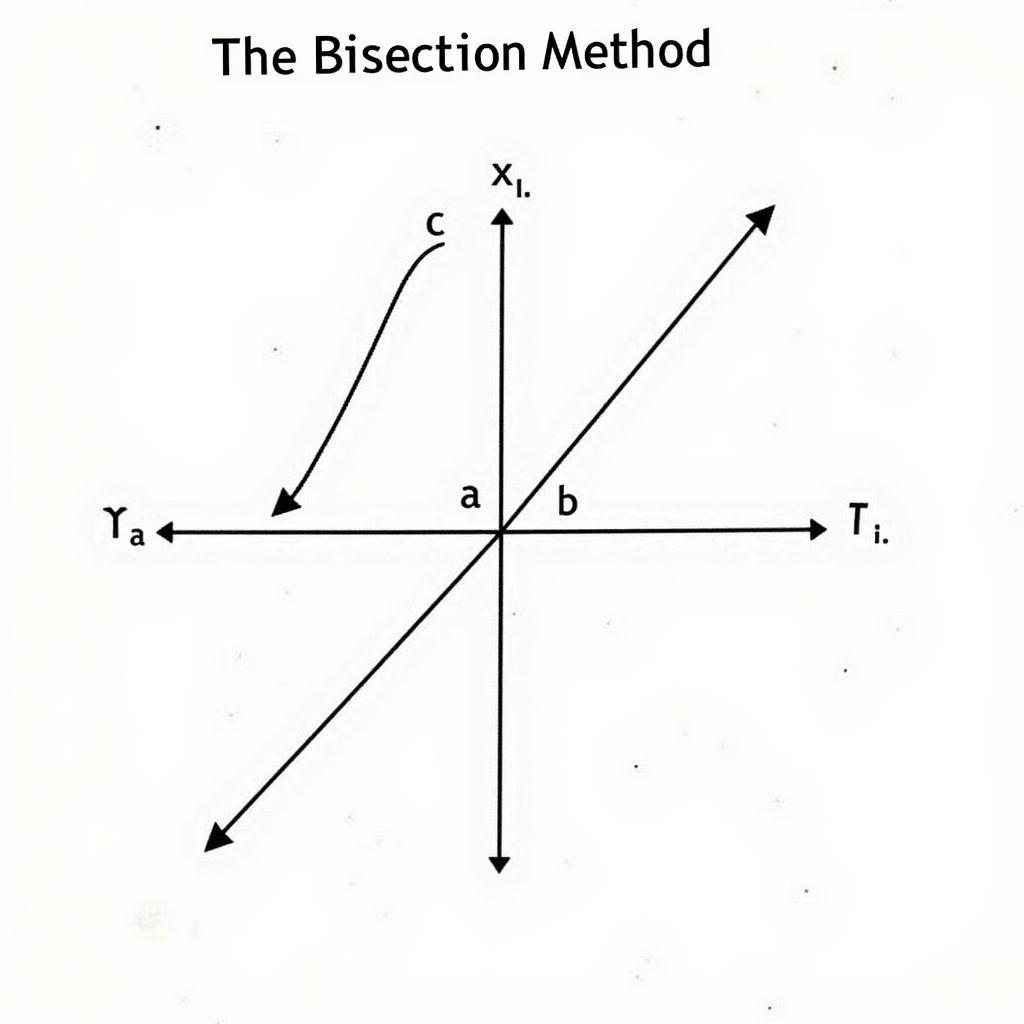Minh họa nguyên lý phương pháp chia đôi that contains the root. The midpoint c of the interval is calculated, and the function is evaluated at c. If f(c) is close to zero, then c is considered an approximation of the root. Otherwise, the interval is updated to either [a, c] or [c, b] depending on the sign of f(c). This process is repeated until the interval is sufficiently small, indicating that the root has been found with the desired accuracy.]
Các Bước Thực Hiện Giải Phương Trình Bằng Phương Pháp Chia Đôi
Để giải phương trình f(x) = 0 bằng phương pháp chia đôi, ta thực hiện các bước sau:
- Xác định khoảng phân ly nghiệm: Tìm hai giá trị a và b sao cho f(a) * f(b) < 0.
- Tính trung điểm: Tính c = (a + b) / 2.
- Kiểm tra nghiệm:
- Nếu f(c) = 0 hoặc |f(c)| < ε (ε là sai số cho phép), thì c là nghiệm gần đúng.
- Nếu f(a) * f(c) < 0, đặt b = c.
- Nếu f(b) * f(c) < 0, đặt a = c.
- Lặp lại bước 2 và 3: Cho đến khi đạt được độ chính xác mong muốn.
Ví Dụ Giải Phương Trình Bằng Phương Pháp Chia Đôi
Giả sử ta muốn giải phương trình x² – 2 = 0. Ta chọn a = 1 và b = 2. Vì f(1) = -1 và f(2) = 2, nên f(1) * f(2) < 0.
- Lần 1: c = (1 + 2) / 2 = 1.5, f(1.5) = 0.25. Vì f(1) * f(1.5) < 0, nên b = 1.5.
- Lần 2: c = (1 + 1.5) / 2 = 1.25, f(1.25) = -0.4375. Vì f(1.25) * f(1.5) < 0, nên a = 1.25.
Cứ tiếp tục như vậy cho đến khi đạt được độ chính xác mong muốn.
. The steps of the bisection method are shown, including calculating the midpoint of the interval and evaluating the function at the midpoint. The process continues until the desired accuracy is achieved, with the final approximation of the root highlighted.]
Ưu và Nhược Điểm của Phương Pháp Chia Đôi
Ưu điểm:
- Đơn giản, dễ thực hiện.
- Luôn hội tụ đến nghiệm nếu khoảng phân ly nghiệm được xác định đúng.
Nhược điểm:
- Hội tụ chậm hơn so với một số phương pháp số khác.
- Khó áp dụng cho phương trình có nhiều nghiệm gần nhau.
Ứng Dụng của Phương Pháp Chia Đôi
Phương pháp chia đôi được ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
- Tìm nghiệm của phương trình đại số và siêu việt.
- Tối ưu hóa hàm số.
- Xử lý tín hiệu.
- Đồ họa máy tính.
Kết luận
Giải phương trình bằng phương pháp chia đôi là một công cụ hữu ích trong toán học và khoa học máy tính. Mặc dù có nhược điểm là hội tụ chậm, nhưng tính đơn giản và khả năng hội tụ đảm bảo của nó khiến nó trở thành một lựa chọn phổ biến cho nhiều ứng dụng.
FAQ
-
Phương pháp chia đôi có thể áp dụng cho phương trình nào?
Phương pháp chia đôi áp dụng cho phương trình có hàm số liên tục và có khoảng phân ly nghiệm.
-
Làm thế nào để chọn khoảng phân ly nghiệm?
Vẽ đồ thị hàm số hoặc thử các giá trị khác nhau cho đến khi tìm được hai giá trị a và b sao cho f(a) * f(b) < 0.
-
Khi nào nên dừng quá trình lặp trong phương pháp chia đôi?
Khi đạt được độ chính xác mong muốn hoặc khi |f(c)| đủ nhỏ.
-
Phương pháp chia đôi có luôn hội tụ không?
Có, nếu khoảng phân ly nghiệm được xác định đúng.
-
Phương pháp chia đôi có nhanh hơn phương pháp Newton-Raphson không?
Không, phương pháp Newton-Raphson thường hội tụ nhanh hơn.
-
Có thể áp dụng phương pháp chia đôi cho phương trình có nhiều nghiệm không?
Có thể, nhưng cần xác định từng khoảng phân ly nghiệm cho mỗi nghiệm.
-
Phương pháp chia đôi có khó thực hiện bằng máy tính không?
Không, phương pháp chia đôi dễ dàng thực hiện bằng các ngôn ngữ lập trình.
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường gặp khó khăn trong việc xác định khoảng phân ly nghiệm và lựa chọn sai số cho phép.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các phương pháp số khác như phương pháp Newton-Raphson, phương pháp dây cung,… trên website của chúng tôi.
