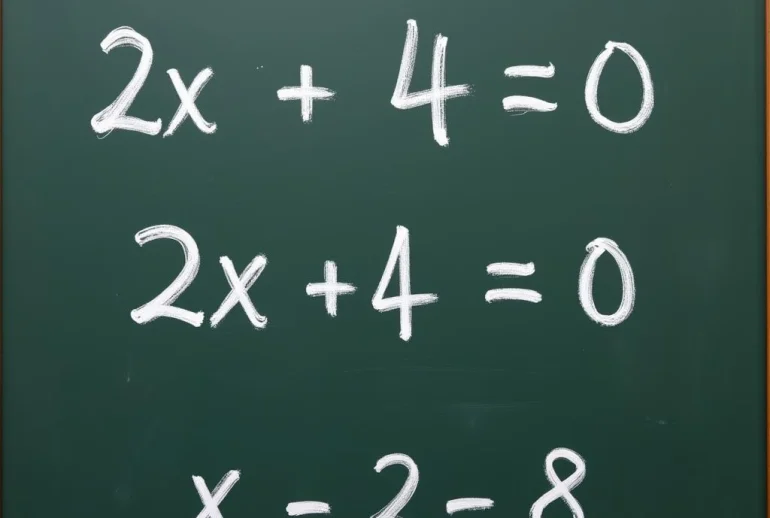Việc giải bài tìm x là một trong những kỹ năng cơ bản và quan trọng nhất trong toán học. Từ những phương trình đơn giản đến những bài toán phức tạp, nắm vững Cách Giải Bài Tìm X sẽ giúp bạn chinh phục mọi thử thách. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết, từ cơ bản đến nâng cao, về cách giải bài tìm x, cùng với những ví dụ minh họa cụ thể và những mẹo nhỏ giúp bạn giải quyết bài toán một cách hiệu quả.
Phương trình bậc nhất một ẩn: Bước đầu tiên trong hành trình tìm x
Phương trình bậc nhất một ẩn có dạng ax + b = 0 (với a ≠ 0). Để giải phương trình này, ta thực hiện các bước sau:
- Chuyển vế số hạng b sang vế phải, đổi dấu thành -b: ax = -b
- Chia cả hai vế cho a (với a ≠ 0): x = -b/a
Ví dụ: Giải phương trình 2x + 4 = 0
- Chuyển vế số hạng 4: 2x = -4
- Chia cả hai vế cho 2: x = -4/2 = -2
Vậy nghiệm của phương trình là x = -2.
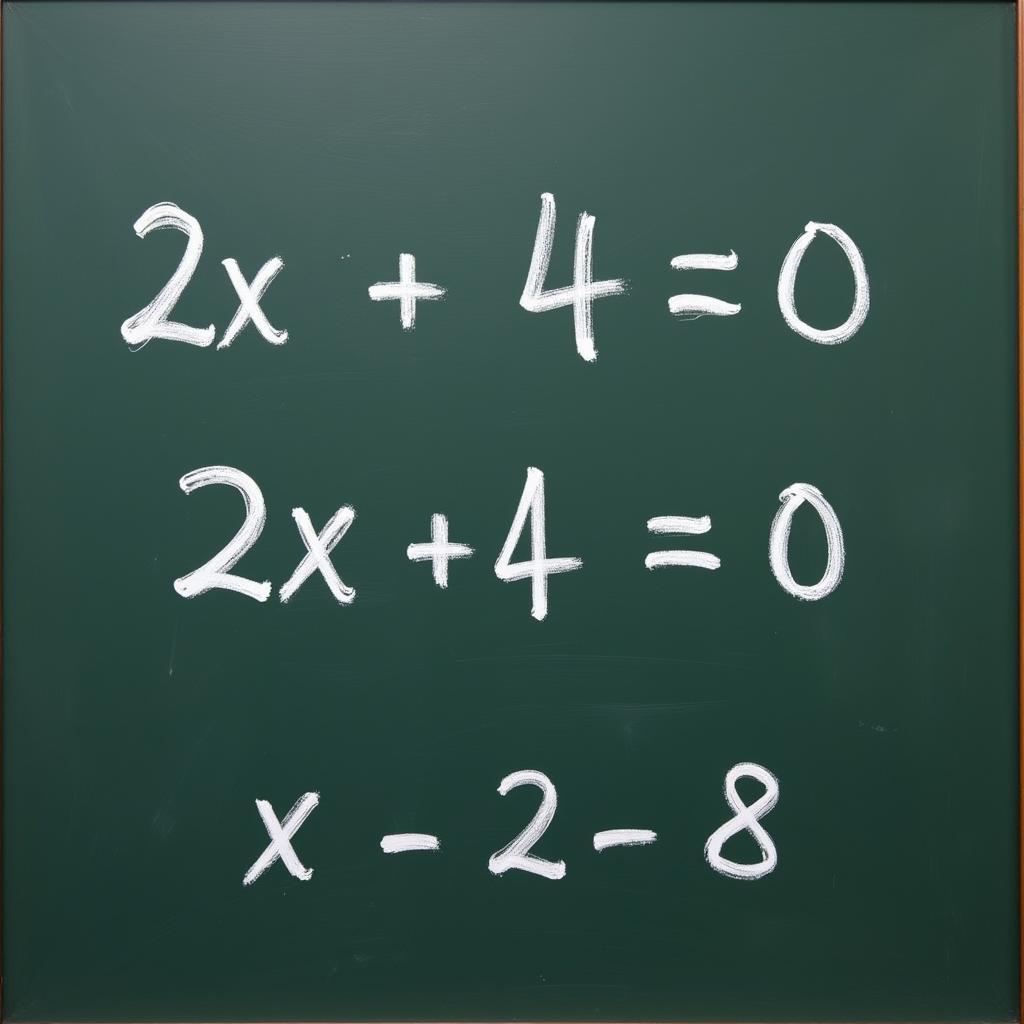Giải phương trình bậc nhất một ẩn
Phương trình bậc hai một ẩn: Nâng cao kỹ năng giải bài tìm x
Phương trình bậc hai một ẩn có dạng ax² + bx + c = 0 (với a ≠ 0). Có nhiều cách để giải phương trình này, bao gồm sử dụng công thức nghiệm, phân tích thành nhân tử, hoặc hoàn thành bình phương.
Công thức nghiệm của phương trình bậc hai: x = (-b ± √(b² – 4ac)) / 2a
Ví dụ: Giải phương trình x² – 3x + 2 = 0
Áp dụng công thức nghiệm: x = (3 ± √((-3)² – 4 1 2)) / 2 * 1 = (3 ± √1) / 2
Vậy nghiệm của phương trình là x = 1 hoặc x = 2.
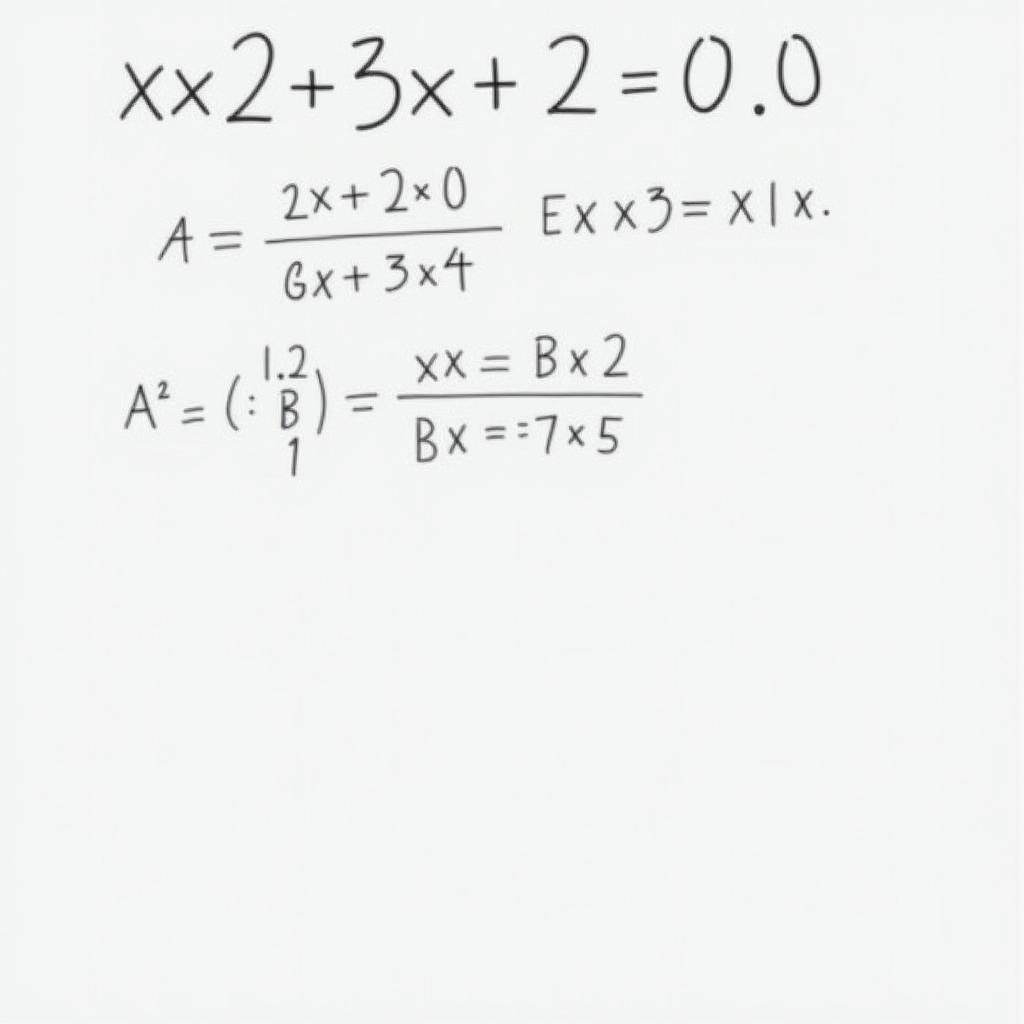Giải phương trình bậc hai một ẩn
Hệ phương trình: Giải bài tìm x trong hệ thống liên kết
Hệ phương trình bao gồm hai hoặc nhiều phương trình có chung ẩn. Có nhiều phương pháp để giải hệ phương trình, chẳng hạn như phương pháp thế, phương pháp cộng đại số.
Ví dụ: Giải hệ phương trình:
x + y = 5
x – y = 1
Sử dụng phương pháp cộng đại số:
(x + y) + (x – y) = 5 + 1
2x = 6
x = 3
Thay x = 3 vào phương trình x + y = 5, ta có:
3 + y = 5
y = 2
Vậy nghiệm của hệ phương trình là x = 3, y = 2.
Giải hệ phương trình
Xem thêm: cách giải bài toán tìm giá trị nhỏ nhất và cách giải bài tập tìm m để bpt vô nghiệm để nâng cao kỹ năng giải toán của bạn.
Mẹo nhỏ giúp bạn giải bài tìm x hiệu quả
- Kiểm tra kỹ các phép tính để tránh sai sót.
- Rèn luyện thường xuyên để nâng cao kỹ năng.
- Nắm vững các quy tắc và công thức cơ bản.
Kết luận: Chinh phục mọi bài toán tìm x
Bài viết này đã cung cấp cho bạn những kiến thức cơ bản và nâng cao về cách giải bài tìm x. Hy vọng rằng, với những hướng dẫn chi tiết và ví dụ minh họa, bạn sẽ tự tin hơn trong việc giải quyết các bài toán tìm x. Hãy luyện tập thường xuyên và áp dụng những mẹo nhỏ để đạt được kết quả tốt nhất. Đừng quên tham khảo thêm cách giải bài tập tìm hạng của ma trận và cách giải bài hóa tìm ctpt để mở rộng kiến thức của mình.
FAQ: Giải đáp những thắc mắc về cách giải bài tìm x
- Khi nào phương trình bậc nhất một ẩn vô nghiệm?
- Làm thế nào để phân biệt phương trình bậc nhất và bậc hai?
- Phương pháp nào hiệu quả nhất để giải hệ phương trình?
- Có những công cụ trực tuyến nào hỗ trợ giải bài tìm x?
- Làm thế nào để kiểm tra kết quả giải bài tìm x?
- Tại sao việc giải bài tìm x lại quan trọng trong toán học?
- Có những ứng dụng thực tế nào của việc giải bài tìm x?
Mô tả các tình huống thường gặp câu hỏi về cách giải bài tìm x
Học sinh thường gặp khó khăn khi giải các phương trình chứa căn bậc hai, giá trị tuyệt đối, hoặc các phương trình có chứa tham số. Việc nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để giải quyết những bài toán này.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về cách giải bài tập tìm khối lượng của nguyên tử.
Khi cần hỗ trợ hãy liên hệ
Email: Contact@badaovl.us, địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
