Giải Bài Tập 64 Trang 136 Sgk Toán 7 là một trong những bài toán hình học quan trọng, giúp học sinh lớp 7 nắm vững kiến thức về tam giác cân, tam giác đều và các tính chất liên quan. Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cho bài tập 64 trang 136 toán 7, cùng với những kiến thức bổ trợ và ví dụ minh họa giúp bạn chinh phục dạng bài này.
Giải Chi Tiết Bài Tập 64 Trang 136 SGK Toán 7
Bài 64 trang 136 sgk toán 7 yêu cầu chứng minh một tam giác là tam giác cân hoặc tam giác đều dựa trên các dữ kiện đã cho. Thông thường, bài toán sẽ cung cấp thông tin về các góc hoặc các cạnh của tam giác, và yêu cầu học sinh vận dụng các định lý và tính chất đã học để chứng minh.
Để giải bài tập 64 trang 136 toán 7, ta cần nắm vững các kiến thức sau:
- Định nghĩa tam giác cân: Tam giác cân là tam giác có hai cạnh bằng nhau.
- Tính chất tam giác cân: Trong tam giác cân, hai góc ở đáy bằng nhau.
- Định nghĩa tam giác đều: Tam giác đều là tam giác có ba cạnh bằng nhau.
- Tính chất tam giác đều: Tam giác đều có ba góc bằng nhau, mỗi góc bằng 60 độ.
Tùy vào dữ kiện cụ thể của bài toán, ta sẽ áp dụng các định lý và tính chất phù hợp để chứng minh. Ví dụ, nếu bài toán cho hai góc của tam giác bằng nhau, ta có thể kết luận tam giác đó là tam giác cân. Nếu bài toán cho ba cạnh của tam giác bằng nhau, ta có thể kết luận tam giác đó là tam giác đều.
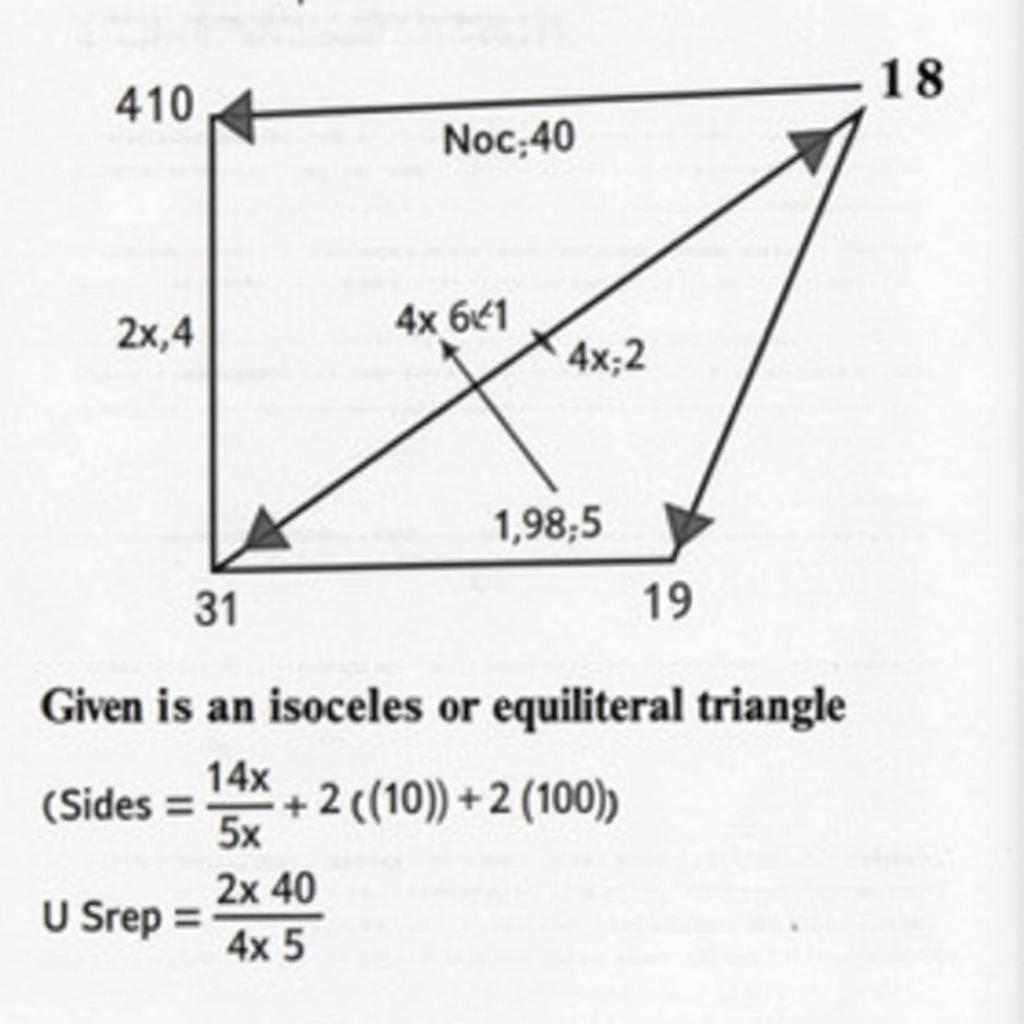Giải Bài Tập 64 Trang 136 Toán 7 Hình 1
Ví Dụ Giải Bài Tập 64 Trang 136 Toán 7
Để hiểu rõ hơn cách giải bài tập 64 trang 136 sgk toán 7, chúng ta cùng xem xét một ví dụ cụ thể.
Đề bài: Cho tam giác ABC có góc A = 60 độ và góc B = góc C. Chứng minh tam giác ABC là tam giác đều.
Lời giải:
Ta có: Tổng ba góc trong một tam giác bằng 180 độ.
=> Góc A + Góc B + Góc C = 180 độ
=> 60 độ + Góc B + Góc C = 180 độ
=> Góc B + Góc C = 120 độ
Vì Góc B = Góc C, nên 2 * Góc B = 120 độ
=> Góc B = 60 độ
=> Góc C = 60 độ
Vậy tam giác ABC có ba góc bằng nhau, mỗi góc bằng 60 độ. Do đó, tam giác ABC là tam giác đều.
Mở Rộng Kiến Thức Về Tam Giác Cân Và Tam Giác Đều
Ngoài việc giải bài tập 64 trang 136 sgk toán 7, việc nắm vững các kiến thức mở rộng về tam giác cân và tam giác đều sẽ giúp bạn giải quyết nhiều bài toán hình học phức tạp hơn.
Ví dụ, đường trung tuyến ứng với cạnh đáy của tam giác cân cũng là đường cao, đường phân giác và đường trung trực. Trong tam giác đều, trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp trùng nhau.
“Việc hiểu rõ các định nghĩa và tính chất cơ bản của tam giác cân và tam giác đều là chìa khóa để giải quyết các bài toán hình học ở bậc trung học cơ sở,” – Nguyễn Văn A, Giáo viên Toán có 15 năm kinh nghiệm chia sẻ.
Kết luận
Giải bài tập 64 trang 136 sgk toán 7 không chỉ giúp bạn nắm vững kiến thức về tam giác cân và tam giác đều mà còn rèn luyện tư duy logic và kỹ năng giải toán. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn trong việc giải quyết các bài toán hình học.
FAQ
- Làm thế nào để phân biệt tam giác cân và tam giác đều?
- Đường trung tuyến trong tam giác cân có tính chất gì đặc biệt?
- Tam giác đều có mấy trục đối xứng?
- Trọng tâm của tam giác đều có vị trí như thế nào?
- Làm thế nào để chứng minh một tam giác là tam giác cân?
- Làm thế nào để chứng minh một tam giác là tam giác đều?
- Ứng dụng của tam giác cân và tam giác đều trong thực tế là gì?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc xác định đúng định lý và tính chất cần áp dụng để chứng minh một tam giác là tam giác cân hoặc tam giác đều. Việc vẽ hình chính xác và phân tích dữ kiện bài toán cũng là một yếu tố quan trọng để giải quyết bài toán thành công.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài tập liên quan đến tam giác cân và tam giác đều tại chuyên mục Toán 7 trên website BaDaoVl.
