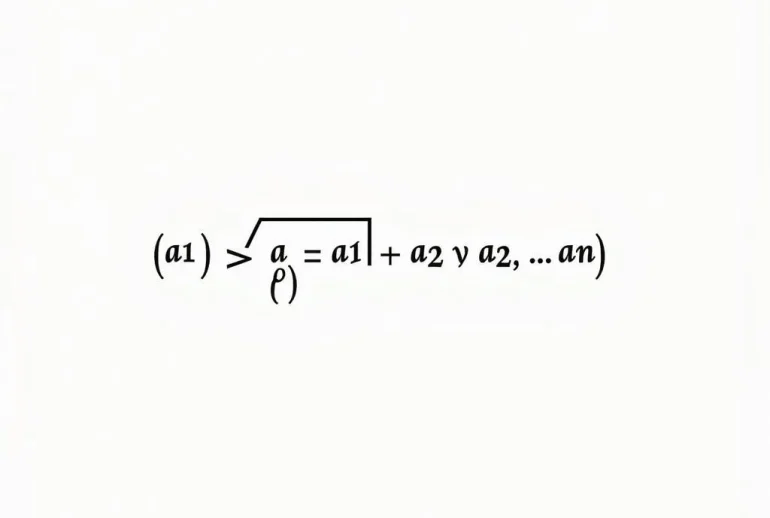Bất phương trình Côsi là một công cụ mạnh mẽ trong giải toán, đặc biệt là trong các bài toán chứng minh bất đẳng thức. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan về Bài Giải Bất Phương Trình Côsi, từ những kiến thức cơ bản đến các kỹ thuật nâng cao, giúp bạn tự tin chinh phục dạng bài toán này.
Bất Đẳng Thức Côsi là gì?
Bất đẳng thức Côsi, hay còn gọi là bất đẳng thức AM-GM (Arithmetic Mean – Geometric Mean), phát biểu rằng trung bình cộng của một tập hợp các số không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng. Dấu bằng xảy ra khi và chỉ khi tất cả các số bằng nhau. Công thức chung của bất đẳng thức Côsi cho n số không âm a1, a2,…, an là:
(a1 + a2 + … + an)/n ≥ n√(a1a2…an)
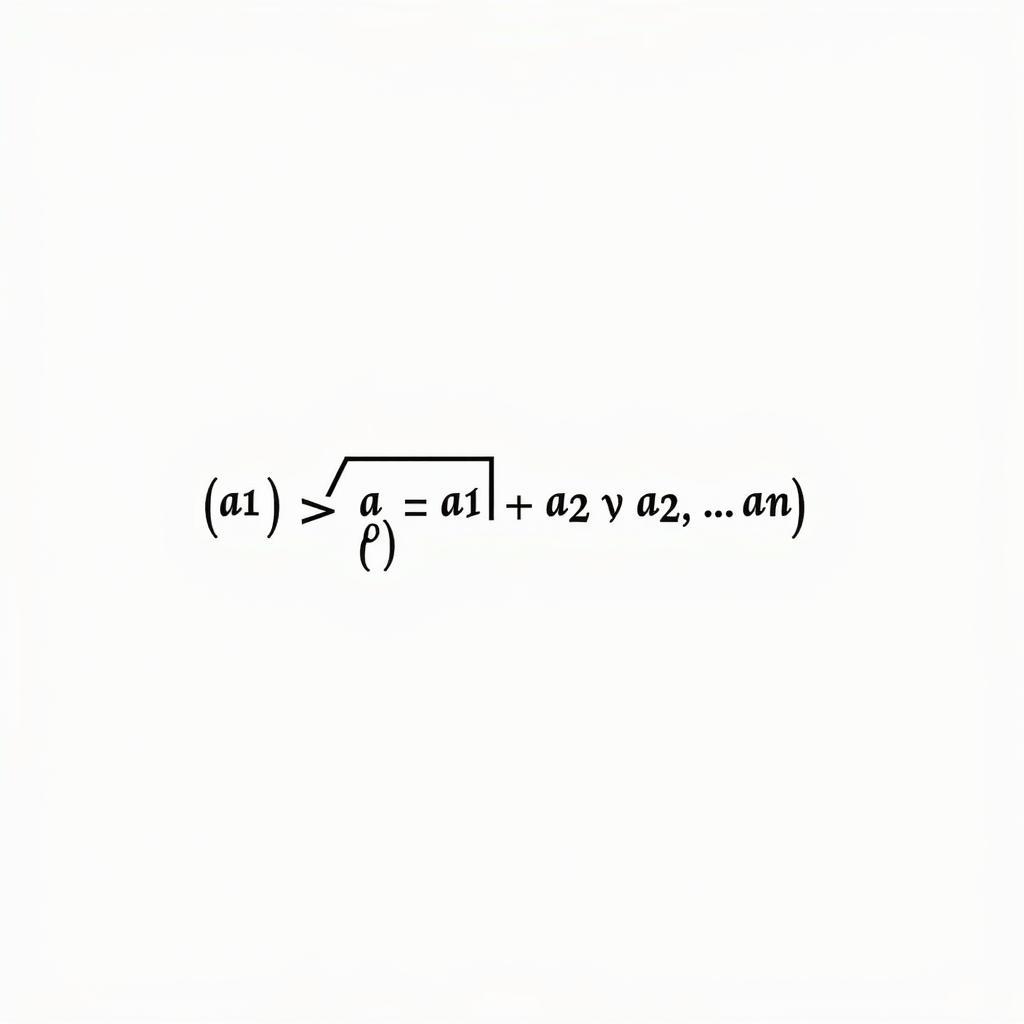Công thức bất đẳng thức Côsi cơ bản
Ứng Dụng Bất Đẳng Thức Côsi trong Giải Bất Phương Trình
Bất đẳng thức Côsi được sử dụng rộng rãi để giải các bài toán bất phương trình. Về cơ bản, ta sẽ áp dụng bất đẳng thức Côsi cho các số hạng trong bất phương trình để tìm ra mối quan hệ giữa chúng và từ đó chứng minh bất phương trình.
Các Dạng Bài Tập Bất Phương Trình Côsi Thường Gặp
- Dạng 1: Chứng minh bất đẳng thức: Đây là dạng bài tập phổ biến nhất. Bạn sẽ được yêu cầu chứng minh một bất đẳng thức cho trước bằng cách áp dụng bất đẳng thức Côsi.
- Dạng 2: Tìm giá trị lớn nhất, nhỏ nhất: Bất đẳng thức Côsi cũng giúp tìm giá trị lớn nhất, nhỏ nhất của một biểu thức. Dấu bằng trong bất đẳng thức Côsi cho ta biết khi nào biểu thức đạt giá trị lớn nhất hoặc nhỏ nhất.
- Dạng 3: Giải bất phương trình: Dạng bài này yêu cầu tìm tập nghiệm của một bất phương trình bằng cách sử dụng bất đẳng thức Côsi.
Ví dụ Giải Bài Tập
Chứng minh rằng với mọi x, y > 0, ta có: x/y + y/x ≥ 2
Lời giải:
Áp dụng bất đẳng thức Côsi cho hai số dương x/y và y/x, ta có:
(x/y + y/x)/2 ≥ √((x/y)*(y/x)) = √1 = 1
Nhân cả hai vế với 2, ta được:
x/y + y/x ≥ 2
Dấu bằng xảy ra khi và chỉ khi x/y = y/x, tức là x = y.
giải bài tập cơ lưu chất sách tiếng anh
Kỹ Thuật Nâng Cao trong Giải Bất Phương Trình Côsi
- Côsi ngược dấu: Kỹ thuật này áp dụng khi ta muốn tìm giá trị nhỏ nhất của một biểu thức có dạng tổng của các phân số.
- Côsi với trọng số: Kỹ thuật này cho phép ta áp dụng bất đẳng thức Côsi cho các số hạng có trọng số khác nhau.
- Côsi cho nhiều số: Áp dụng bất đẳng thức Côsi cho nhiều hơn hai số.
Lời khuyên khi giải bài tập bất phương trình Côsi:
- Xác định rõ dạng bài tập và mục tiêu của bài toán.
- Nhận biết các số hạng nào có thể áp dụng bất đẳng thức Côsi.
- Kiểm tra điều kiện dấu bằng.
Kết luận
Bài giải bất phương trình Côsi đòi hỏi sự am hiểu về bất đẳng thức Côsi và các kỹ thuật áp dụng. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán liên quan đến bất phương trình Côsi. Nắm vững những kiến thức này, bạn sẽ tự tin hơn trong việc chinh phục dạng bài toán này. giải bài 1 sgk hóa 9 trang 144
FAQ
- Bất đẳng thức Côsi áp dụng cho những số nào? Số không âm
- Khi nào dấu bằng trong bất đẳng thức Côsi xảy ra? Khi tất cả các số bằng nhau
- Côsi ngược dấu là gì? Kỹ thuật áp dụng khi tìm giá trị nhỏ nhất của tổng các phân số
- Côsi với trọng số là gì? Kỹ thuật áp dụng khi các số hạng có trọng số khác nhau
- Làm thế nào để nhận biết khi nào nên áp dụng bất đẳng thức Côsi? Quan sát dạng của bất phương trình và các số hạng
- Tại sao cần kiểm tra điều kiện dấu bằng? Để đảm bảo lời giải đầy đủ và chính xác
- Có những tài liệu nào khác về bất đẳng thức Côsi? giải vở bài tập tiếng anh 7
Mô tả các tình huống thường gặp câu hỏi. Ví dụ như khi nào cần dùng Côsi ngược dấu, khi nào cần dùng Côsi với trọng số.
Gợi ý các câu hỏi khác, bài viết khác có trong web. Ví dụ như bài viết về bất đẳng thức Bunhiacopxki, bất đẳng thức Holder.
Khi cần hỗ trợ hãy liên hệ Email: Contact@badaovl.us, địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
