Bài Giải Chương 2 đại Số Tuyến Tính Ntu là chủ đề được nhiều sinh viên quan tâm, đặc biệt là những bạn đang theo học tại trường Đại học Nguyễn Tất Thành (NTU). Chương này thường tập trung vào các khái niệm quan trọng như không gian vectơ, độc lập tuyến tính, phụ thuộc tuyến tính, cơ sở và chiều. Nắm vững kiến thức chương này là nền tảng để học tốt các chương tiếp theo.
Khái Niệm Cơ Bản về Không Gian Vectơ
Không gian vectơ là một tập hợp các vectơ cùng với hai phép toán: cộng vectơ và nhân vectơ với một số vô hướng. Để hiểu rõ hơn về không gian vectơ, ta cần nắm vững các tính chất của nó như tính đóng, tính kết hợp, tính giao hoán, sự tồn tại của vectơ không và vectơ đối. Việc hiểu rõ định nghĩa và các tính chất này giúp sinh viên dễ dàng giải quyết các bài toán liên quan đến không gian vectơ.
Độc Lập Tuyến Tính và Phụ Thuộc Tuyến Tính
Một tập hợp các vectơ được gọi là độc lập tuyến tính nếu không có vectơ nào trong tập hợp đó có thể được biểu diễn dưới dạng tổ hợp tuyến tính của các vectơ còn lại. Ngược lại, nếu có một vectơ có thể được biểu diễn dưới dạng tổ hợp tuyến tính của các vectơ khác, thì tập hợp các vectơ đó được gọi là phụ thuộc tuyến tính. Phân biệt được hai khái niệm này là rất quan trọng trong việc xác định cơ sở của một không gian vectơ.
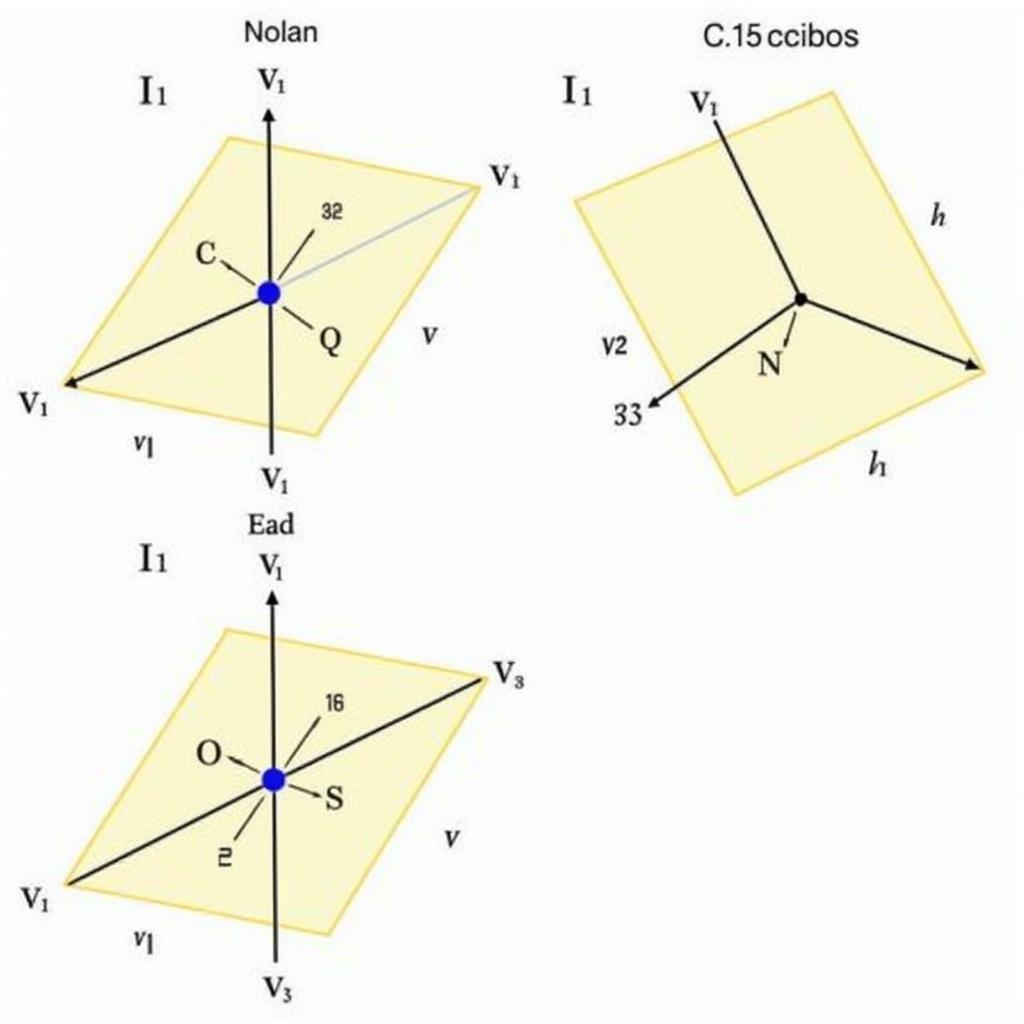Minh họa độc lập và phụ thuộc tuyến tính
Cơ Sở và Chiều của Không Gian Vectơ
Cơ sở của một không gian vectơ là một tập hợp các vectơ độc lập tuyến tính mà span ra toàn bộ không gian đó. Chiều của không gian vectơ là số lượng vectơ trong một cơ sở bất kỳ của nó. Việc tìm cơ sở và xác định chiều của không gian vectơ là một trong những bài toán quan trọng trong chương 2 đại số tuyến tính NTU.
Xác Định Cơ Sở và Chiều
Để xác định cơ sở và chiều của một không gian vectơ, ta có thể sử dụng phương pháp biến đổi ma trận. Bằng cách biến đổi ma trận về dạng bậc thang, ta có thể tìm ra các vectơ độc lập tuyến tính và từ đó xác định cơ sở và chiều của không gian vectơ.
Ông Nguyễn Văn A, Giảng viên Đại số Tuyến Tính tại NTU, chia sẻ: “Việc nắm vững khái niệm cơ sở và chiều là rất quan trọng, nó giúp sinh viên hiểu sâu hơn về cấu trúc của không gian vectơ.”
Bài Tập Áp Dụng
Chương 2 đại số tuyến tính NTU thường bao gồm nhiều bài tập áp dụng, từ cơ bản đến nâng cao, giúp sinh viên củng cố kiến thức. Các bài tập này thường yêu cầu sinh viên xác định không gian vectơ, kiểm tra độc lập tuyến tính, tìm cơ sở và chiều của không gian vectơ.
Bà Trần Thị B, Trợ giảng Đại số Tuyến Tính tại NTU, cho biết: “Sinh viên nên làm nhiều bài tập để nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.”
Kết luận
Bài giải chương 2 đại số tuyến tính NTU cung cấp cho sinh viên những kiến thức nền tảng quan trọng về không gian vectơ, độc lập tuyến tính, phụ thuộc tuyến tính, cơ sở và chiều. Nắm vững các khái niệm này sẽ giúp sinh viên học tốt các chương tiếp theo của môn học.
FAQ
- Không gian vectơ là gì?
- Làm thế nào để kiểm tra độc lập tuyến tính của một tập hợp các vectơ?
- Cơ sở của một không gian vectơ là gì?
- Chiều của không gian vectơ được định nghĩa như thế nào?
- Tại sao việc học bài giải chương 2 đại số tuyến tính NTU lại quan trọng?
- Làm thế nào để tìm cơ sở của một không gian vectơ?
- Có những phương pháp nào để xác định chiều của một không gian vectơ?
Mô tả các tình huống thường gặp câu hỏi
Sinh viên thường gặp khó khăn trong việc xác định độc lập tuyến tính và phụ thuộc tuyến tính của một tập hợp các vectơ, cũng như tìm cơ sở và chiều của không gian vectơ.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm thấy các bài viết liên quan đến các chương khác của đại số tuyến tính trên website BaDaoVl.
Khi cần hỗ trợ hãy liên hệ Email: Contact@badaovl.us, địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
