Bài Giải Toán Lớp 9 Tập 1 là nền tảng quan trọng cho việc học toán ở cấp trung học cơ sở. Nắm vững kiến thức trong tập 1 sẽ giúp học sinh tự tin chinh phục những bài toán khó hơn ở các tập sau và chuẩn bị tốt cho kỳ thi vào lớp 10. Bài viết này sẽ cung cấp cho bạn những hướng dẫn chi tiết, bài tập minh họa và tài liệu tham khảo hữu ích để học tốt toán lớp 9 tập 1.
Đại Số Lớp 9 Tập 1: Khám Phá Thế Giới Căn Bậc Hai và Hàm Số
Phần đại số lớp 9 tập 1 chủ yếu xoay quanh các khái niệm về căn bậc hai, hàm số bậc nhất và hàm số bậc hai. Đây là những kiến thức nền tảng cho việc học toán ở các lớp trên.
Căn bậc hai: Từ Định Nghĩa đến Ứng Dụng
Căn bậc hai là một khái niệm quan trọng trong toán học. Hiểu rõ định nghĩa và tính chất của căn bậc hai sẽ giúp bạn giải quyết nhiều bài toán phức tạp. Ngoài ra, việc luyện tập thường xuyên các bài tập về căn bậc hai sẽ giúp bạn nâng cao kỹ năng tính toán và tư duy logic.
- Định nghĩa căn bậc hai số học của một số không âm a là số x không âm sao cho x² = a.
- Tính chất của căn bậc hai: √(a.b) = √a . √b (với a ≥ 0, b ≥ 0); √(a/b) = √a / √b (với a ≥ 0, b > 0).
Bài Giải Toán Lớp 9 Tập 1: Minh họa Căn Bậc Hai
Hàm số bậc nhất: Đường thẳng và Bài Toán Thực Tế
Hàm số bậc nhất có dạng y = ax + b (a ≠ 0). Đồ thị của hàm số bậc nhất là một đường thẳng. Việc vẽ đồ thị và tìm hiểu các tính chất của hàm số bậc nhất sẽ giúp bạn giải quyết các bài toán liên quan đến đường thẳng trong mặt phẳng tọa độ.
- Cách vẽ đồ thị hàm số bậc nhất: Lấy hai điểm bất kỳ thuộc đồ thị hàm số, sau đó nối hai điểm đó lại ta được đồ thị hàm số.
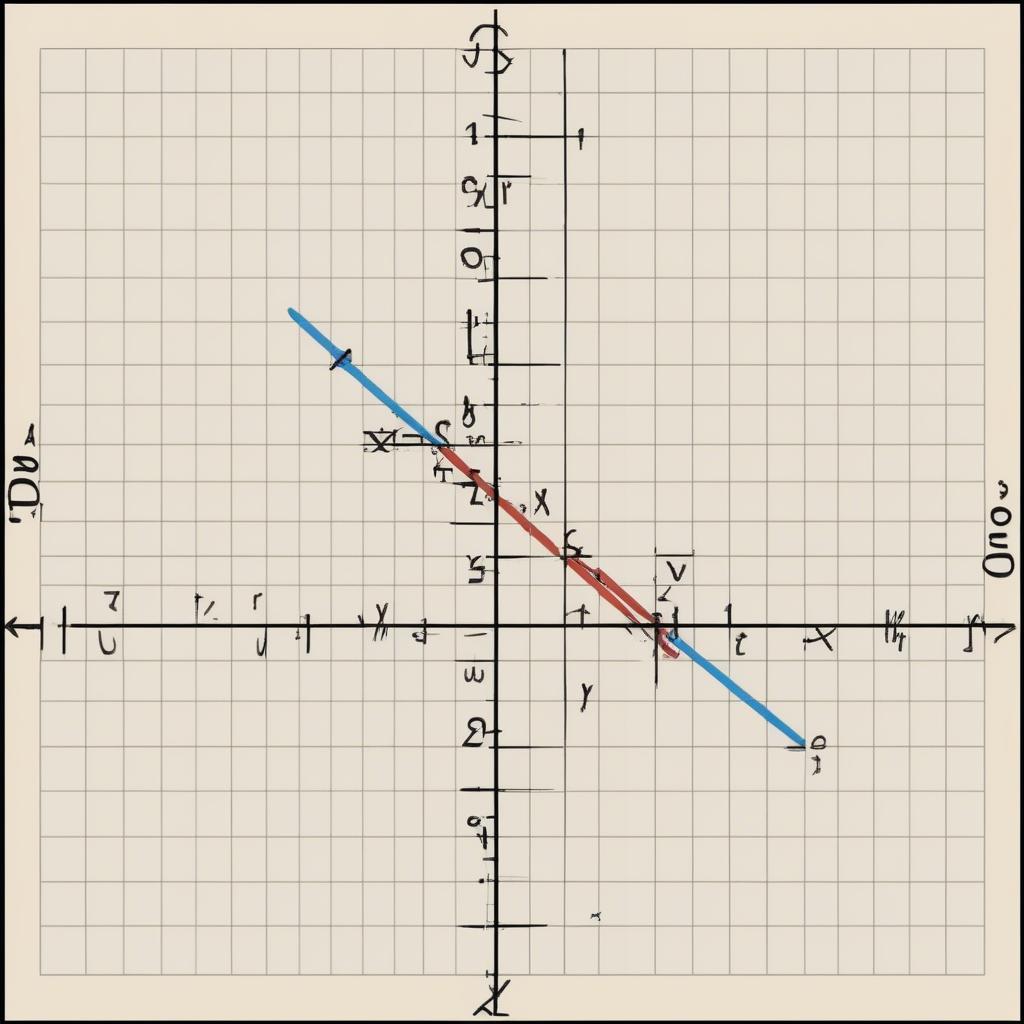Bài Giải Toán Lớp 9 Tập 1: Đồ thị Hàm Số Bậc Nhất
Hàm số bậc hai: Parabol và Ứng Dụng
Hàm số bậc hai có dạng y = ax² + bx + c (a ≠ 0). Đồ thị của hàm số bậc hai là một parabol. Việc nắm vững kiến thức về hàm số bậc hai sẽ giúp bạn giải quyết các bài toán liên quan đến parabol và các ứng dụng của nó trong thực tế.
- Đỉnh của parabol: I(-b/2a; -Δ/4a) với Δ = b² – 4ac.
“Học sinh cần nắm vững các công thức và tính chất của hàm số bậc hai để giải quyết các bài toán liên quan đến đỉnh, trục đối xứng, và giao điểm của parabol với các trục tọa độ.” – Nguyễn Văn A, Giáo viên Toán.
Hình Học Lớp 9 Tập 1: Hệ Thức Lượng Trong Tam Giác Vuông
Hình học lớp 9 tập 1 tập trung vào hệ thức lượng trong tam giác vuông. Đây là một phần kiến thức quan trọng, giúp học sinh làm quen với các định lý và công thức liên quan đến tam giác vuông.
Định Lý Pytago: Công cụ đắc lực cho tam giác vuông
Định lý Pytago là một định lý cơ bản trong hình học, phát biểu rằng trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Định lý này có nhiều ứng dụng trong việc tính toán độ dài các cạnh của tam giác vuông.
- Định lý Pytago: a² + b² = c² (với c là cạnh huyền, a và b là hai cạnh góc vuông).
Bài Giải Toán Lớp 9 Tập 1: Minh họa Định Lý Pytago
“Việc hiểu và áp dụng thành thạo định lý Pytago là chìa khóa để giải quyết nhiều bài toán hình học phức tạp.” – Trần Thị B, Giáo viên Toán.
Kết luận
Bài giải toán lớp 9 tập 1 bao gồm các kiến thức quan trọng về đại số và hình học, đặt nền tảng cho việc học toán ở các lớp trên. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn trong việc học toán lớp 9.
FAQ
- Làm thế nào để học tốt toán lớp 9 tập 1?
- Tài liệu nào hữu ích cho việc ôn tập toán lớp 9 tập 1?
- Làm sao để nhớ được các công thức toán lớp 9 tập 1?
- Cách giải bài toán hình học lớp 9 tập 1 hiệu quả?
- Ứng dụng của toán lớp 9 tập 1 trong thực tế là gì?
- Làm sao để phân biệt hàm số bậc nhất và hàm số bậc hai?
- Khi nào nên áp dụng định lý Pytago?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc vận dụng các công thức toán học vào giải bài tập. Ví dụ, nhiều bạn chưa nắm vững cách áp dụng định lý Pytago để tính toán độ dài các cạnh trong tam giác vuông. Hoặc, việc xác định đỉnh và trục đối xứng của parabol cũng là một vấn đề mà nhiều học sinh còn lúng túng.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài giải toán lớp 9 tập 2, các đề thi học sinh giỏi toán 9, hoặc các phương pháp học tập hiệu quả trên website của chúng tôi.
