Bài Tập Có Lời Giải Môn Lý Thuyết đồ Thị đóng vai trò then chốt trong việc nắm vững kiến thức và ứng dụng lý thuyết đồ thị vào thực tế. Việc tìm kiếm và luyện tập với các bài tập này sẽ giúp bạn hiểu sâu hơn về các khái niệm, thuật toán và ứng dụng đa dạng của lý thuyết đồ thị.
Lý Thuyết Đồ Thị Là Gì? Và Tại Sao Cần Luyện Bài Tập Có Lời Giải?
Lý thuyết đồ thị là một nhánh của toán học rời rạc, nghiên cứu về các đồ thị, là một cấu trúc toán học dùng để biểu diễn mối quan hệ giữa các đối tượng. Một đồ thị bao gồm các đỉnh (nodes) và các cạnh (edges) nối giữa các đỉnh. Luyện tập bài tập có lời giải môn lý thuyết đồ thị không chỉ giúp bạn kiểm tra kiến thức mà còn rèn luyện tư duy logic và kỹ năng giải quyết vấn đề.
Tầm Quan Trọng Của Bài Tập Có Lời Giải Trong Việc Học Lý Thuyết Đồ Thị
Bài tập có lời giải cung cấp cho bạn cách tiếp cận, phân tích và giải quyết các vấn đề liên quan đến đồ thị. Thông qua việc xem xét lời giải, bạn có thể học hỏi từ những sai lầm của mình, nắm bắt được các phương pháp giải quyết tối ưu và nâng cao khả năng tư duy thuật toán.
Bài tập lý thuyết đồ thị cơ bản
Các Loại Bài Tập Lý Thuyết Đồ Thị Phổ Biến
Có rất nhiều loại bài tập lý thuyết đồ thị khác nhau, từ cơ bản đến nâng cao, bao gồm:
- Tìm đường đi ngắn nhất: Xác định đường đi ngắn nhất giữa hai đỉnh trong đồ thị.
- Cây khung nhỏ nhất: Tìm cây khung nhỏ nhất của một đồ thị.
- Bài toán tô màu đồ thị: Tô màu các đỉnh của đồ thị sao cho không có hai đỉnh kề nhau có cùng màu.
- Luồng cực đại: Tìm luồng cực đại từ một đỉnh nguồn đến một đỉnh đích trong một mạng lưới.
Bài Tập Tìm Đường Đi Ngắn Nhất: Dijkstra và Floyd-Warshall
Hai thuật toán phổ biến để giải quyết bài toán tìm đường đi ngắn nhất là Dijkstra và Floyd-Warshall. Dijkstra được sử dụng cho đồ thị có trọng số không âm, trong khi Floyd-Warshall có thể áp dụng cho cả đồ thị có trọng số âm (miễn là không có chu trình âm).
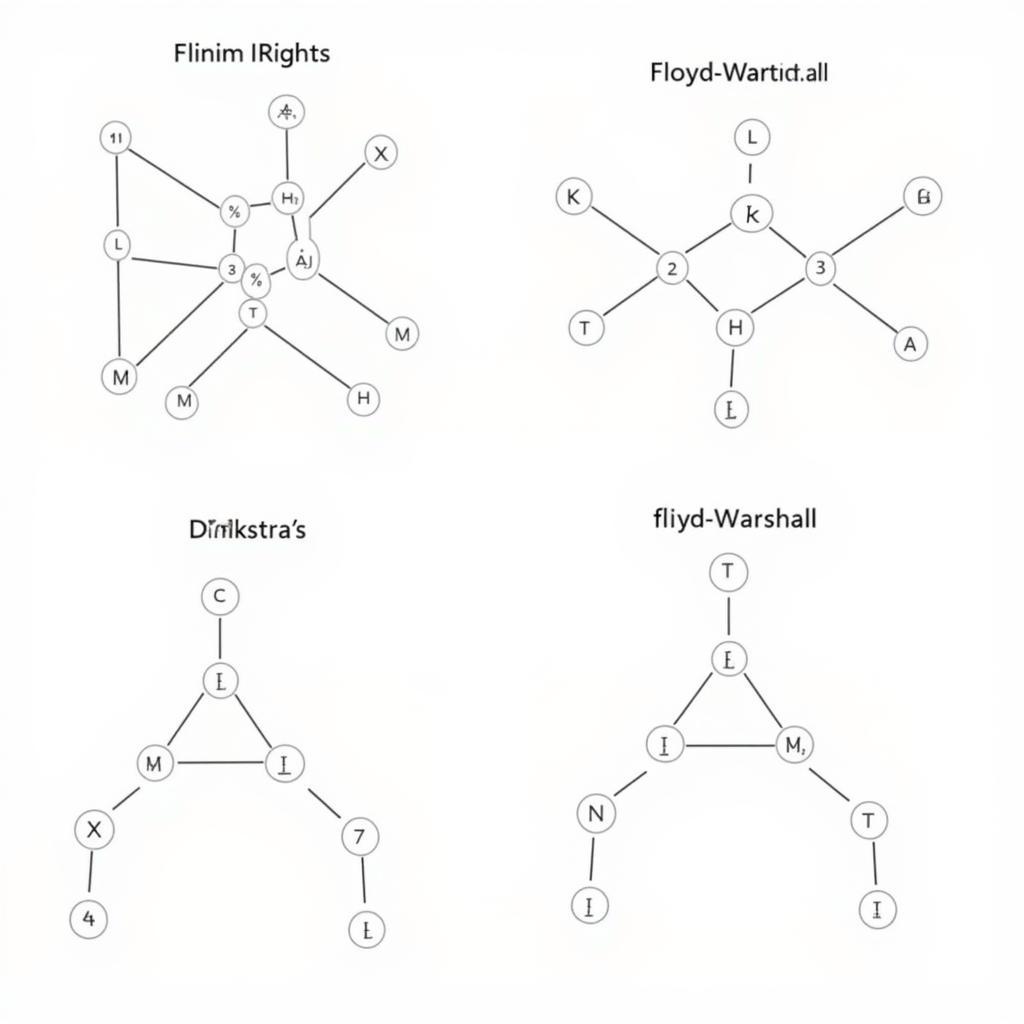Thuật toán Dijkstra và Floyd-Warshall
Lợi Ích Của Việc Thường Xuyên Luyện Tập Bài Tập Có Lời Giải
- Nắm vững kiến thức: Luyện tập giúp củng cố kiến thức lý thuyết và hiểu sâu hơn về các khái niệm.
- Phát triển tư duy: Rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề.
- Ứng dụng thực tế: Lý thuyết đồ thị có ứng dụng rộng rãi trong nhiều lĩnh vực như khoa học máy tính, logistics, mạng xã hội.
Ứng Dụng Của Lý Thuyết Đồ Thị Trong Khoa Học Máy Tính
Lý thuyết đồ thị được ứng dụng rộng rãi trong khoa học máy tính, ví dụ như trong việc thiết kế mạng máy tính, tối ưu hóa thuật toán tìm kiếm, phân tích mạng xã hội.
“Lý thuyết đồ thị là một công cụ mạnh mẽ giúp chúng ta mô hình hóa và giải quyết nhiều vấn đề phức tạp trong thực tế,” – TS. Nguyễn Văn A, Chuyên gia Lý Thuyết Đồ Thị.
Tìm Kiếm Nguồn Tài Liệu Bài Tập Có Lời Giải Môn Lý Thuyết Đồ Thị
Bạn có thể tìm thấy nhiều nguồn tài liệu bài tập có lời giải môn lý thuyết đồ thị trực tuyến, trong sách giáo khoa, hoặc trên các diễn đàn học tập.
Tài liệu bài tập lý thuyết đồ thị
Kết Luận
Bài tập có lời giải môn lý thuyết đồ thị là một phần quan trọng trong quá trình học tập và nghiên cứu. Bằng việc luyện tập thường xuyên, bạn sẽ nắm vững kiến thức, phát triển tư duy và có thể ứng dụng lý thuyết đồ thị vào thực tế.
FAQ
- Lý thuyết đồ thị là gì?
- Tại sao cần luyện tập bài tập có lời giải môn lý thuyết đồ thị?
- Các loại bài tập lý thuyết đồ thị phổ biến là gì?
- Thuật toán Dijkstra và Floyd-Warshall là gì?
- Ứng dụng của lý thuyết đồ thị trong khoa học máy tính là gì?
- Tìm kiếm nguồn tài liệu bài tập có lời giải môn lý thuyết đồ thị ở đâu?
- Làm thế nào để học tốt lý thuyết đồ thị?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc hiểu các khái niệm trừu tượng và áp dụng các thuật toán vào bài tập cụ thể. Việc tìm kiếm bài tập có lời giải chi tiết sẽ giúp học sinh hiểu rõ hơn cách giải quyết vấn đề.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài toán liên quan đến đồ thị như bài toán người bán hàng, bài toán tìm đường đi Euler, bài toán tìm đường đi Hamilton…
