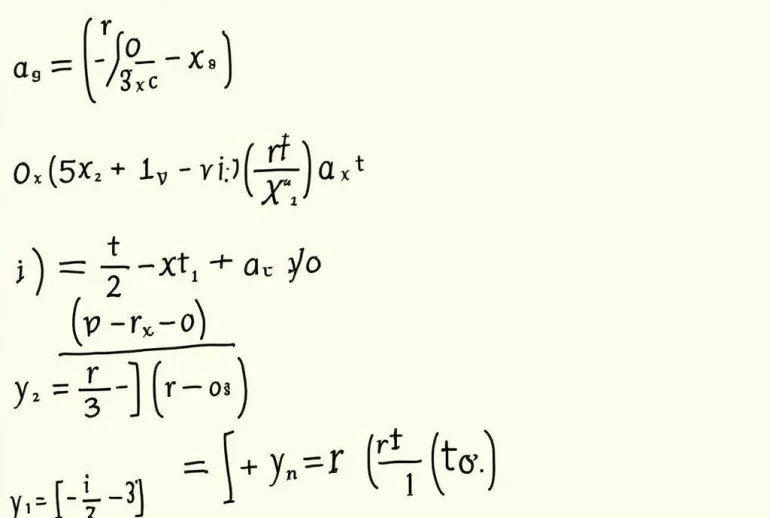Bài Tập Nâng Cao Môn Giải Tích I là thử thách không nhỏ đối với nhiều sinh viên. Nắm vững kiến thức cơ bản và luyện tập thường xuyên là chìa khóa để chinh phục những bài toán khó. Bài viết này sẽ cung cấp cho bạn những phương pháp, kỹ thuật và ví dụ cụ thể để giải quyết các bài tập nâng cao môn Giải tích I một cách hiệu quả.
Nâng Cao Kỹ Năng Giải Bài Tập Nâng Cao Môn Giải Tích I
Giải tích I là nền tảng quan trọng cho các môn học toán cao cấp hơn. Việc thành thạo giải các bài tập nâng cao không chỉ giúp bạn đạt điểm cao trong môn học mà còn rèn luyện tư duy logic và khả năng phân tích vấn đề. Đừng ngại thử sức với những bài toán khó, bởi đó chính là cơ hội để bạn phát triển tư duy toán học của mình.
Bài tập nâng cao Giải Tích I với các công thức phức tạp
Giới Hạn và Đạo Hàm: Từ Cơ Bản Đến Nâng Cao
Hai khái niệm cốt lõi trong Giải tích I là giới hạn và đạo hàm. Bài tập nâng cao thường yêu cầu bạn kết hợp nhiều định lý và kỹ thuật để tìm giới hạn hoặc đạo hàm của các hàm số phức tạp. Ví dụ, việc áp dụng quy tắc L’Hopital, định lý kẹp, hoặc khai triển Taylor có thể giúp bạn giải quyết những bài toán tưởng chừng như rất khó.
Tích Phân: Ứng Dụng và Bài Toán Thực Tế
Tích phân là một công cụ mạnh mẽ để tính diện tích, thể tích, và giải quyết nhiều bài toán thực tế. Bài tập nâng cao môn giải tích i thường liên quan đến tích phân suy rộng, tích phân kép, hoặc tích phân đường. Việc hiểu rõ các phương pháp tính tích phân và cách áp dụng chúng vào các tình huống cụ thể là rất quan trọng.
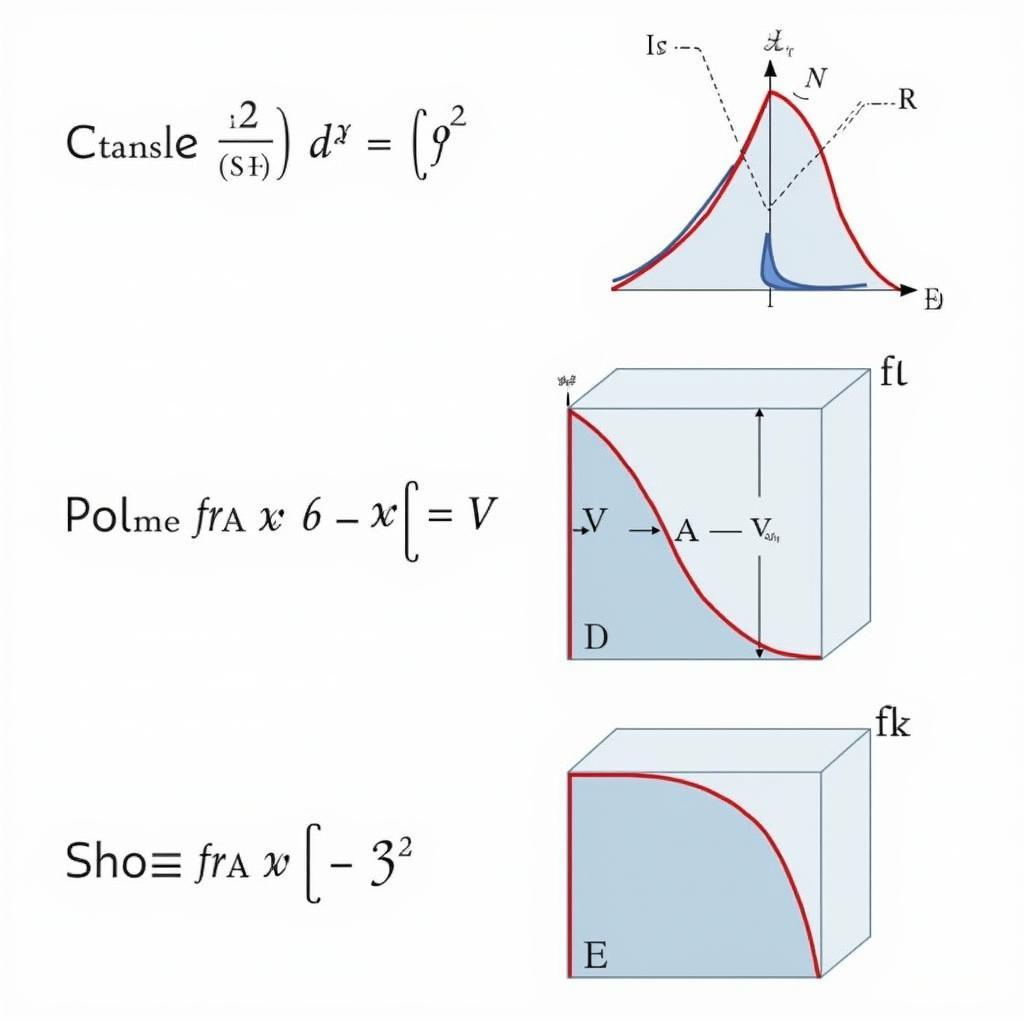Ứng dụng của tích phân trong bài tập Giải tích I
Kỹ Thuật Giải Bài Tập Nâng Cao Môn Giải Tích I
Để giải quyết các bài tập nâng cao, bạn cần nắm vững các kỹ thuật sau:
- Phân tích đề bài: Đọc kỹ đề bài, xác định yêu cầu của bài toán, và liệt kê các thông tin đã cho.
- Vẽ hình: Hình vẽ minh họa có thể giúp bạn hình dung bài toán và tìm ra hướng giải quyết.
- Sử dụng các định lý và công thức: Áp dụng các định lý và công thức đã học để biến đổi và rút gọn biểu thức.
- Kiểm tra kết quả: Sau khi tìm ra đáp án, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
giải bài 37 38 39 sgk toán 9 tập 2
Ví Dụ Bài Tập Nâng Cao Môn Giải Tích I
Xét hàm số f(x) = (sin x)/x. Tìm giới hạn của f(x) khi x tiến tới 0.
Giải:
Áp dụng quy tắc L’Hopital, ta có:
lim(x→0) (sin x)/x = lim(x→0) (cos x)/1 = cos(0) = 1
giải vở bài tập toán lớp 5 bài 69
Luyện Tập Thường Xuyên Là Chìa Khóa Thành Công
Giải tích I đòi hỏi sự kiên trì và luyện tập thường xuyên. Hãy dành thời gian làm bài tập mỗi ngày để củng cố kiến thức và nâng cao kỹ năng giải toán. Đừng ngại tìm kiếm sự giúp đỡ từ giảng viên, bạn bè, hoặc các nguồn tài liệu trực tuyến.
giải bài tâp vật lý lớp 9 bài 34
“Thành công trong Giải tích I không đến từ may mắn, mà đến từ sự nỗ lực và kiên trì.” – GS.TS Nguyễn Văn A, chuyên gia Giải tích.
Kết Luận
Bài tập nâng cao môn giải tích i là một thử thách, nhưng cũng là cơ hội để bạn phát triển tư duy toán học và nâng cao kiến thức. Hãy áp dụng các kỹ thuật và phương pháp đã học, luyện tập thường xuyên, và đừng ngại tìm kiếm sự giúp đỡ khi cần thiết. Chúc bạn thành công!
“Việc giải quyết các bài tập nâng cao giúp sinh viên hiểu sâu hơn về bản chất của Giải tích I.” – TS. Lê Thị B, giảng viên Đại học C.
FAQ
- Làm thế nào để bắt đầu học Giải tích I?
- Tài liệu nào hữu ích cho việc học Giải tích I?
- Làm sao để vượt qua nỗi sợ hãi khi gặp bài tập nâng cao?
- Có những phần mềm hỗ trợ học Giải tích I nào?
- Tầm quan trọng của Giải tích I trong các ngành khoa học kỹ thuật là gì?
- Làm thế nào để tìm gia sư Giải tích I?
- Có những khóa học online về Giải tích I nào?
Mô tả các tình huống thường gặp câu hỏi.
Sinh viên thường gặp khó khăn khi áp dụng các định lý và công thức vào bài tập cụ thể. Việc luyện tập nhiều bài tập đa dạng sẽ giúp sinh viên quen với các dạng bài và cách áp dụng lý thuyết.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như “Ứng dụng của đạo hàm”, “Tích phân từng phần”, “Phương trình vi phân” trên website của chúng tôi.
