Bất phương trình bậc nhất hai ẩn là một phần quan trọng trong chương trình Toán THCS và THPT. Nắm vững cách giải bài tập bất phương trình bậc nhất hai ẩn không chỉ giúp bạn đạt điểm cao mà còn rèn luyện tư duy logic và khả năng phân tích vấn đề. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về bất phương trình bậc nhất hai ẩn, giải bài tập từ cơ bản đến nâng cao, cùng với những mẹo hay giúp bạn chinh phục dạng toán này.
Định nghĩa Bất Phương Trình Bậc Nhất Hai Ẩn
Bất phương trình bậc nhất hai ẩn x và y có dạng tổng quát là ax + by + c > 0 (hoặc ax + by + c < 0, ax + by + c ≥ 0, ax + by + c ≤ 0), với a, b, c là các số thực, a và b không đồng thời bằng 0. Tập nghiệm của bất phương trình bậc nhất hai ẩn là một miền trên mặt phẳng tọa độ Oxy.
Cách Giải Bất Phương Trình Bậc Nhất Hai Ẩn
Để giải bất phương trình bậc nhất hai ẩn, ta thực hiện các bước sau:
- Biến đổi bất phương trình về dạng ax + by + c > 0 (hoặc < 0, ≥ 0, ≤ 0).
- Vẽ đường thẳng ax + by + c = 0. Đường thẳng này chia mặt phẳng tọa độ thành hai miền.
- Lấy một điểm bất kỳ không thuộc đường thẳng (thường là gốc tọa độ O(0,0) nếu O không nằm trên đường thẳng).
- Thay tọa độ điểm đó vào bất phương trình.
- Nếu bất phương trình đúng, miền chứa điểm đó là miền nghiệm.
- Nếu bất phương trình sai, miền không chứa điểm đó là miền nghiệm.
- Biểu diễn miền nghiệm bằng cách gạch bỏ miền không phải là nghiệm. Đường thẳng ax + by + c = 0 được vẽ nét liền nếu bất phương trình có dấu ≥ hoặc ≤, và vẽ nét đứt nếu bất phương trình có dấu > hoặc <.
 Giải bất phương trình bậc nhất hai ẩn bước 1
Giải bất phương trình bậc nhất hai ẩn bước 1
Ví dụ Giải Bất Phương Trình Bậc Nhất Hai Ẩn
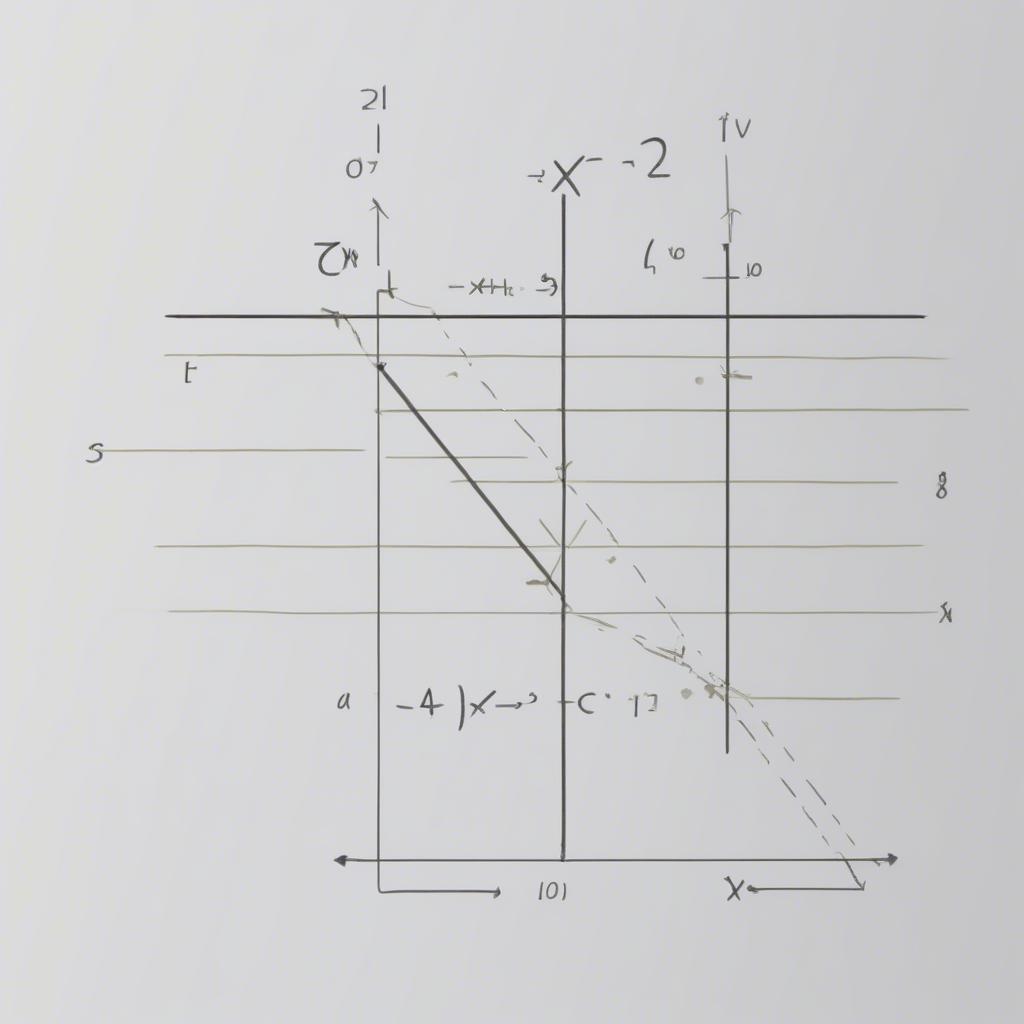
Xét bất phương trình 2x – y + 1 > 0.
- Bất phương trình đã ở dạng chuẩn.
- Vẽ đường thẳng 2x – y + 1 = 0.
- Lấy điểm O(0,0). Thay vào bất phương trình ta được 1 > 0 (đúng).
- Vậy miền nghiệm là nửa mặt phẳng chứa O(0,0).
 Giải bất phương trình bậc nhất hai ẩn ví dụ
Giải bất phương trình bậc nhất hai ẩn ví dụ
Hệ Bất Phương Trình Bậc Nhất Hai Ẩn
Hệ bất phương trình bậc nhất hai ẩn là tập hợp nhiều bất phương trình bậc nhất hai ẩn. Miền nghiệm của hệ là giao của các miền nghiệm của từng bất phương trình trong hệ.
Ví dụ Giải Hệ Bất Phương Trình Bậc Nhất Hai Ẩn
Xét hệ bất phương trình:
x + y - 2 ≤ 0
x - 2y + 1 ≥ 0Ta vẽ đường thẳng x + y – 2 = 0 và x – 2y + 1 = 0. Sau đó xác định miền nghiệm của từng bất phương trình. Miền nghiệm của hệ là phần giao của hai miền nghiệm.
 Giải hệ bất phương trình bậc nhất hai ẩn
Giải hệ bất phương trình bậc nhất hai ẩn
Kết luận
Bất Phương Trình Bậc Nhất Hai ẩn Giải Bài Tập là một dạng toán quan trọng. Hiểu rõ định nghĩa, cách giải và luyện tập thường xuyên sẽ giúp bạn thành thạo dạng toán này.
FAQ
-
Tập nghiệm của bất phương trình bậc nhất hai ẩn là gì?
Tập nghiệm là một miền trên mặt phẳng tọa độ.
-
Làm thế nào để xác định miền nghiệm?
Bằng cách thử một điểm bất kỳ vào bất phương trình.
-
Miền nghiệm của hệ bất phương trình là gì?
Là giao của các miền nghiệm của từng bất phương trình.
-
Khi nào vẽ đường thẳng nét liền, khi nào vẽ nét đứt?
Nét liền khi dấu ≥ hoặc ≤, nét đứt khi dấu > hoặc <.
-
Bất phương trình bậc nhất hai ẩn có bao nhiêu ẩn?
Có hai ẩn.
-
Có thể tìm nghiệm của bất phương trình bậc nhất hai ẩn bằng máy tính không?
Có thể sử dụng phần mềm vẽ đồ thị để hỗ trợ.
-
Làm sao để giải hệ bất phương trình bậc nhất hai ẩn có nhiều hơn hai bất phương trình?
Tương tự như hệ hai bất phương trình, ta tìm giao của tất cả các miền nghiệm.
Bạn muốn tìm hiểu thêm về các dạng bài tập bất phương trình bậc nhất hai ẩn khác? Xem thêm các bài viết liên quan trên BaDaoVl.
Khi cần hỗ trợ hãy liên hệ Email: [email protected], địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.