Nguyên hàm là một khái niệm quan trọng trong giải tích, và việc nắm vững Cách Giải Bài Toán Nguyên Hàm là điều thiết yếu cho học sinh, sinh viên các ngành khoa học kỹ thuật. Bài viết này sẽ cung cấp cho bạn một hướng dẫn chi tiết về cách giải quyết các bài toán nguyên hàm từ cơ bản đến nâng cao.
Nắm Vững Định Nghĩa Nguyên Hàm
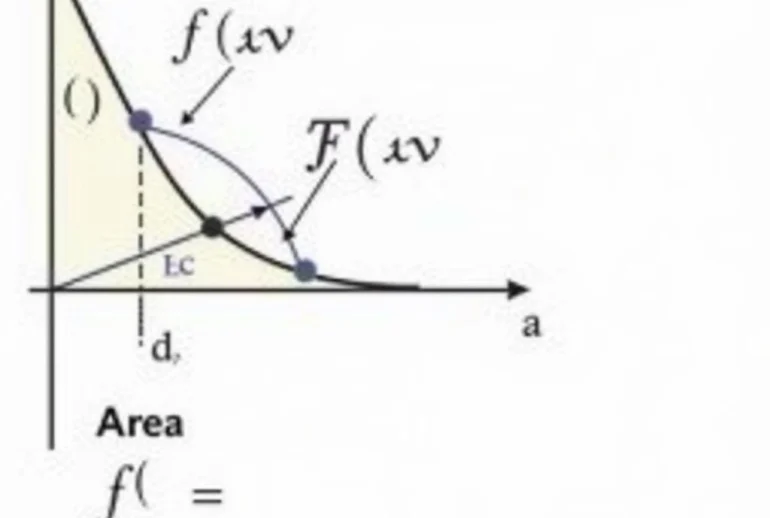
Trước khi đi vào cách giải bài toán nguyên hàm, chúng ta cần hiểu rõ định nghĩa của nó. Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x). Nói cách khác, F’(x) = f(x). Việc tìm nguyên hàm còn được gọi là phép tính tích phân không xác định.
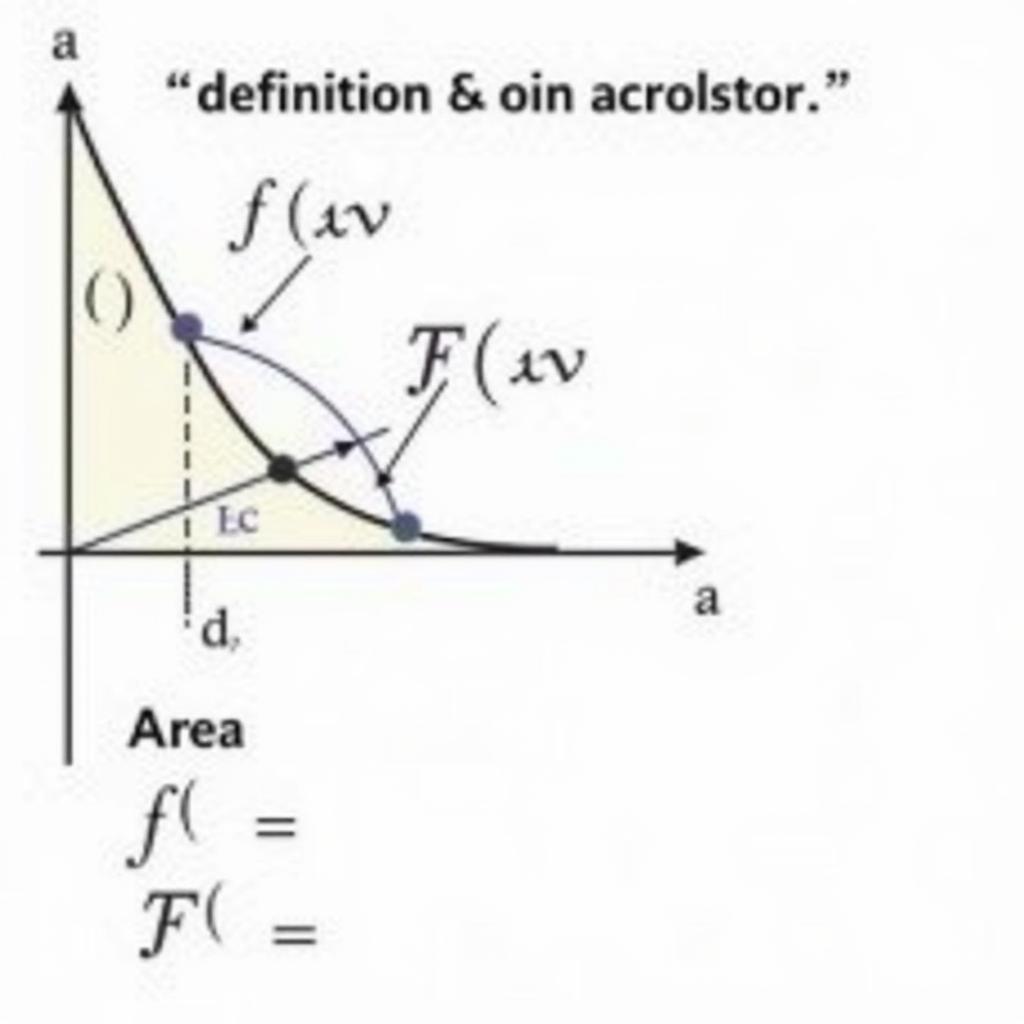Nguyên hàm định nghĩa
Các Phương Pháp Giải Nguyên Hàm Cơ Bản
Có một số phương pháp cơ bản để giải bài toán nguyên hàm. Dưới đây là một số phương pháp phổ biến nhất:
- Công thức nguyên hàm cơ bản: Ghi nhớ các công thức nguyên hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit là bước đầu tiên quan trọng.
- Phương pháp đổi biến: Kỹ thuật này cho phép chúng ta đơn giản hóa tích phân bằng cách thay đổi biến.
- Phương pháp tích phân từng phần: Phương pháp này hữu ích khi giải quyết tích phân của tích hai hàm số.
Phương pháp giải nguyên hàm cơ bản
Giải Quyết Các Bài Toán Nguyên Hàm Nâng Cao
Khi đã nắm vững các phương pháp cơ bản, bạn có thể tiếp cận các bài toán nguyên hàm phức tạp hơn. Một số kỹ thuật nâng cao bao gồm:
- Tích phân hàm phân thức: Đây là loại tích phân liên quan đến các phân số của các đa thức.
- Tích phân hàm lượng giác: Sử dụng các công thức lượng giác để biến đổi và giải quyết tích phân.
- Tích phân hàm vô tỉ: Loại tích phân này liên quan đến các căn thức.
Ví dụ Minh Họa Cách Giải Bài Toán Nguyên Hàm
Để hiểu rõ hơn về cách giải bài toán nguyên hàm, chúng ta hãy xem một ví dụ cụ thể. Tìm nguyên hàm của hàm số f(x) = x^2 + 2x + 1. Áp dụng công thức nguyên hàm cơ bản, ta có F(x) = (1/3)x^3 + x^2 + x + C, với C là hằng số tích phân.
Kết Luận
Cách giải bài toán nguyên hàm đòi hỏi sự kết hợp giữa việc nắm vững lý thuyết và luyện tập thường xuyên. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết các bài toán nguyên hàm một cách hiệu quả. Hãy bắt đầu thực hành ngay hôm nay!
FAQ
- Nguyên hàm là gì?
- Làm thế nào để tìm nguyên hàm của một hàm số?
- Phương pháp đổi biến là gì?
- Khi nào nên sử dụng phương pháp tích phân từng phần?
- Hằng số tích phân C có ý nghĩa gì?
- Làm thế nào để kiểm tra kết quả tính nguyên hàm?
- Có tài liệu nào hữu ích để học thêm về nguyên hàm không?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn khi xác định phương pháp phù hợp để giải một bài toán nguyên hàm. Việc phân biệt khi nào nên dùng phương pháp đổi biến, tích phân từng phần, hay các kỹ thuật khác thường gây nhầm lẫn.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về bài toán về tổng ti hiệu tỉ không có giải, giải bài toán lớp 3 bài, bài giải lớp 4, và các bài tập hình họa có lời giải. Ngoài ra, bài viết giải sách bài tập vật lí 7 bài 11 cũng có thể hữu ích.
