Giải Bài 4 Trang 130 Sgk Toán 8 Tập 2 là một trong những bài toán quan trọng trong chương trình hình học lớp 8, giúp học sinh nắm vững kiến thức về diện tích hình thang. Bài viết này sẽ cung cấp lời giải chi tiết, bài tập vận dụng và những kiến thức bổ trợ giúp bạn chinh phục bài toán này một cách dễ dàng.
Hiểu Rõ Về Bài Toán 4 Trang 130 SGK Toán 8 Tập 2
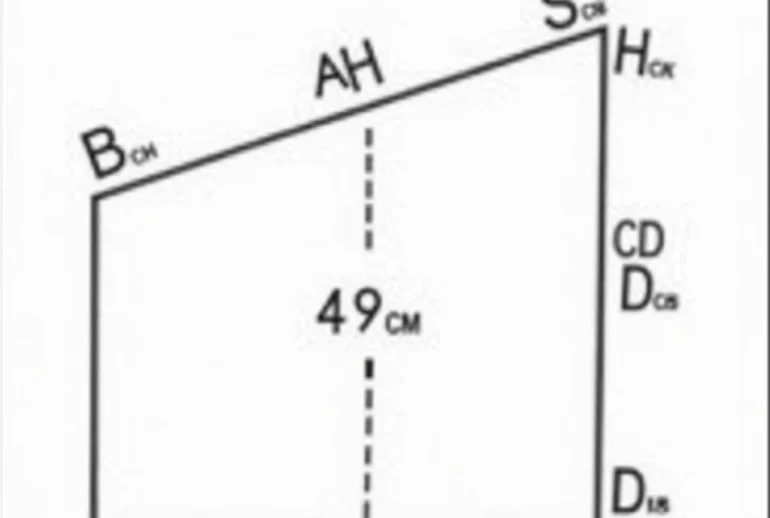
Bài toán yêu cầu tính diện tích hình thang ABCD có AB // CD, AB = 9cm, BC = 15cm, CD = 13cm, AD = 12cm. Để giải bài toán này, chúng ta cần vận dụng công thức tính diện tích hình thang và một số kiến thức về tam giác vuông.
Hướng Dẫn Giải Chi Tiết Bài 4 Trang 130 SGK Toán 8 Tập 2
- Bước 1: Kẻ đường cao. Từ A kẻ AH vuông góc với CD, từ B kẻ BK vuông góc với CD. Ta có AH = BK là chiều cao của hình thang ABCD.
- Bước 2: Tính độ dài DH và CK. Ta thấy DH = (CD – AB)/2 do ABKH là hình chữ nhật. Thay số vào ta được DH = (13 – 9)/2 = 2cm. CK cũng bằng 2cm.
- Bước 3: Áp dụng định lý Pytago. Trong tam giác vuông ADH, ta có AD² = AH² + DH². Suy ra AH² = AD² – DH² = 12² – 2² = 140. Vậy AH = √140 = 2√35 cm.
- Bước 4: Tính diện tích hình thang. Diện tích hình thang ABCD được tính theo công thức: S = (AB + CD) AH / 2. Thay số vào ta được S = (9 + 13) 2√35 / 2 = 22√35 cm².
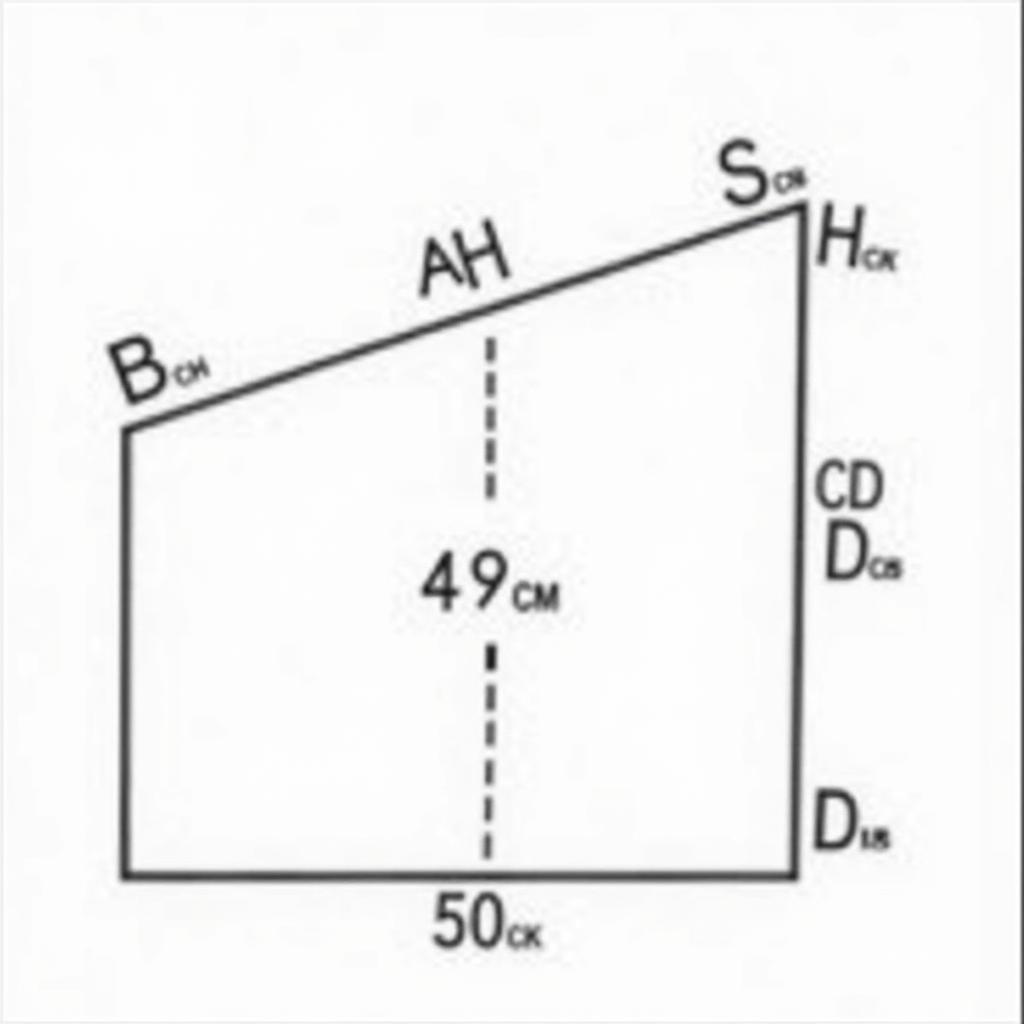Giải Bài 4 Trang 130 SGK Toán 8 Tập 2 Hình vẽ minh họa
Bài Tập Vận Dụng Giải Bài 4 Trang 130 SGK Toán 8 Tập 2
- Một hình thang có đáy lớn 15cm, đáy nhỏ 11cm, chiều cao 8cm. Tính diện tích hình thang đó.
- Một hình thang có diện tích 120cm², đáy lớn 14cm, đáy nhỏ 10cm. Tính chiều cao của hình thang.
Mở Rộng Kiến Thức Về Diện Tích Hình Thang
Diện tích hình thang được tính bằng nửa tổng hai đáy nhân với chiều cao. Công thức chung là S = (a + b) * h / 2, trong đó a và b là độ dài hai đáy, h là chiều cao.
Giải Đáp Một Số Câu Hỏi Thường Gặp
Làm thế nào để xác định chiều cao của hình thang?
Chiều cao của hình thang là khoảng cách vuông góc giữa hai đáy. Bạn có thể kẻ đường cao từ một đỉnh của đáy nhỏ xuống đáy lớn.
Nếu bài toán không cho đủ dữ kiện thì sao?
Nếu bài toán không cho đủ dữ kiện để tính diện tích trực tiếp, bạn cần tìm cách bổ sung thông tin bằng cách áp dụng các định lý hình học như định lý Pytago, hoặc các tính chất của hình thang cân, hình thang vuông.
Lời khuyên từ chuyên gia
Theo Thầy Nguyễn Văn A, giáo viên Toán giàu kinh nghiệm: “Việc nắm vững công thức tính diện tích hình thang là rất quan trọng. Học sinh cần luyện tập nhiều bài tập để thành thạo cách áp dụng công thức và các kiến thức liên quan.”
Cô Phạm Thị B, một chuyên gia giáo dục khác, cũng chia sẻ: “Ngoài việc học thuộc công thức, học sinh nên hiểu rõ bản chất của công thức và cách vận dụng nó trong các tình huống thực tế.”
Kết luận
Giải bài 4 trang 130 SGK toán 8 tập 2 không khó nếu bạn nắm vững công thức tính diện tích hình thang và biết cách vận dụng định lý Pytago. Hy vọng bài viết này đã giúp bạn hiểu rõ cách giải bài toán và áp dụng vào các bài tập tương tự.
FAQ
- Công thức tính diện tích hình thang là gì?
- Làm thế nào để tìm chiều cao của hình thang?
- Định lý Pytago được áp dụng như thế nào trong bài toán này?
- Có những loại hình thang nào?
- Diện tích hình thang cân được tính như thế nào?
- Làm thế nào để phân biệt hình thang cân và hình thang vuông?
- Có những bài tập nào khác tương tự bài 4 trang 130?
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài toán liên quan đến hình học lớp 8 tại BaDaoVl. Hãy khám phá thêm các bài viết về diện tích hình tam giác, hình vuông, hình chữ nhật, và các hình khác.
