Bài 7 trang 134 SGK Toán 9 là một bài tập quan trọng trong chương trình học, giúp học sinh nắm vững kiến thức về hình học không gian, cụ thể là hình nón. Bài viết này sẽ cung cấp lời giải chi tiết và các phương pháp tiếp cận bài toán, cùng với những ví dụ minh họa giúp bạn hiểu rõ hơn về cách Giải Bài 7 Sgk Toán 9 Trang 134.
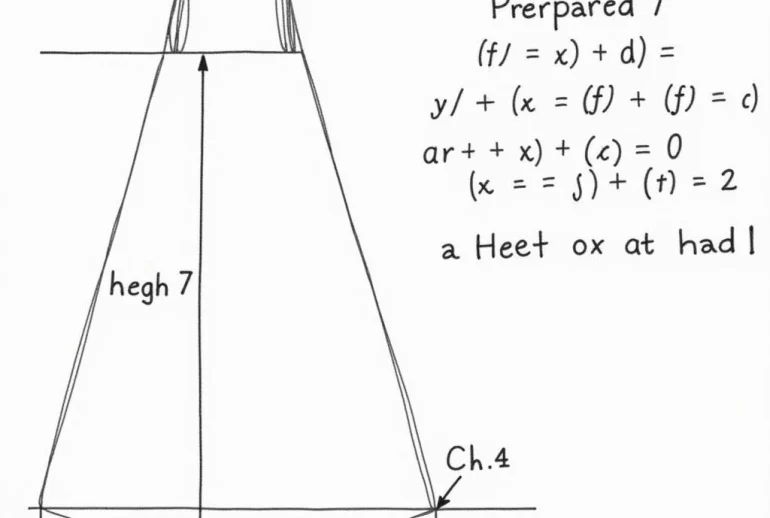
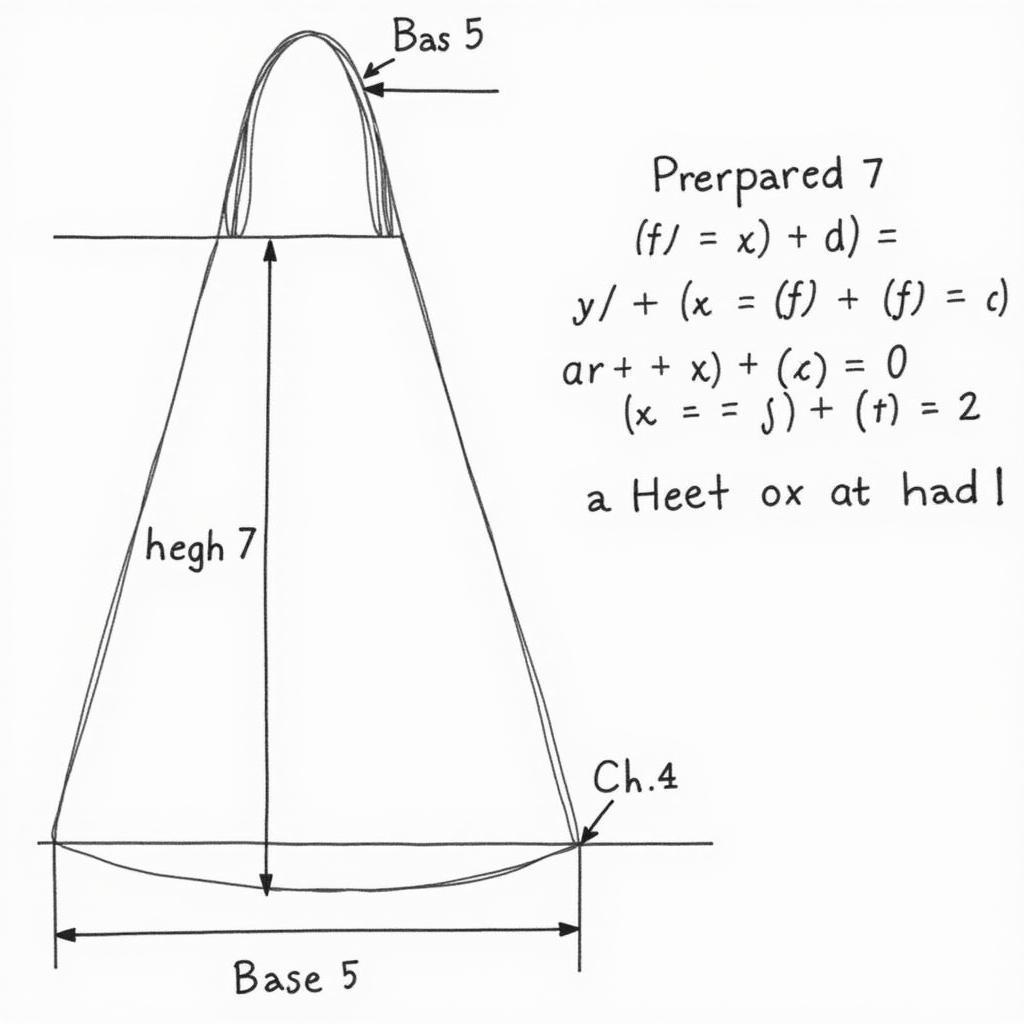Hình nón và các công thức liên quan bài 7 toán 9 trang 134
Tìm Hiểu Bài Toán 7 Trang 134 SGK Toán 9
Thông thường, bài 7 trang 134 SGK Toán 9 yêu cầu tính toán các đại lượng liên quan đến hình nón như bán kính đáy, đường sinh, diện tích xung quanh, diện tích toàn phần và thể tích. Để giải quyết bài toán này, chúng ta cần nắm vững các công thức cơ bản của hình nón. Đầu tiên, hãy cùng xem lại một số khái niệm quan trọng. Hình nón được tạo thành bằng cách quay một tam giác vuông quanh một cạnh góc vuông. Cạnh góc vuông đó trở thành đường cao của hình nón, cạnh huyền là đường sinh, và cạnh góc vuông còn lại là bán kính đáy.
Công Thức Tính Diện Tích Xung Quanh Hình Nón
Diện tích xung quanh của hình nón được tính bằng công thức: Sxq = πrl, trong đó r là bán kính đáy và l là đường sinh.
Công Thức Tính Diện Tích Toàn Phần Hình Nón
Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy: Stp = Sxq + πr².
Công Thức Tính Thể Tích Hình Nón
Thể tích của hình nón được tính bằng công thức: V = (1/3)πr²h, trong đó h là chiều cao của hình nón.
Hướng Dẫn Giải Bài 7 SGK Toán 9 Trang 134
Để giải bài 7 sgk toán 9 trang 134 một cách hiệu quả, chúng ta cần thực hiện theo các bước sau:
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Xác định các đại lượng đã cho và đại lượng cần tìm.
- Vẽ hình minh họa và ghi chú các thông tin đã biết.
- Áp dụng các công thức phù hợp để tính toán các đại lượng cần tìm.
- Kiểm tra lại kết quả và đơn vị đo.
Ví dụ Minh Họa
Cho hình nón có bán kính đáy r = 5cm và đường sinh l = 13cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón.
- Bước 1: Xác định yêu cầu: Tính Sxq, Stp và V.
- Bước 2: Đại lượng đã cho: r = 5cm, l = 13cm. Đại lượng cần tìm: Sxq, Stp, V.
- Bước 3: Vẽ hình nón và ghi chú các thông tin.
- Bước 4: Tính toán: Sxq = πrl = π 5 13 = 65π (cm²); Để tính Stp và V, ta cần tìm chiều cao h. Vì hình nón được tạo thành từ tam giác vuông, ta áp dụng định lý Pytago: h² + r² = l² => h = √(l² – r²) = √(13² – 5²) = 12cm. Stp = Sxq + πr² = 65π + π 5² = 90π (cm²); V = (1/3)πr²h = (1/3)π 5² * 12 = 100π (cm³).
- Bước 5: Kết luận: Sxq = 65π cm², Stp = 90π cm², V = 100π cm³.
Mở Rộng Kiến Thức Về Hình Nón
Hình nón là một hình không gian thú vị với nhiều ứng dụng trong thực tế. Việc nắm vững các công thức và phương pháp giải bài toán liên quan đến hình nón sẽ giúp bạn giải quyết nhiều bài toán phức tạp hơn.
giải bài tập bài 52 sinh học lớp 7
Kết luận
Bài viết đã cung cấp lời giải chi tiết cho bài 7 sgk toán 9 trang 134, cùng với các ví dụ minh họa và phương pháp giải bài toán. Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về hình nón và tự tin hơn trong việc giải các bài tập liên quan. Nắm vững kiến thức này không chỉ giúp bạn đạt điểm cao trong các kỳ thi mà còn giúp bạn phát triển tư duy logic và khả năng giải quyết vấn đề.
bài toán giải tổng 3 góc trong 1 tam giác
FAQ về Bài 7 SGK Toán 9 Trang 134
- Công thức tính diện tích xung quanh hình nón là gì?
- Làm thế nào để tính thể tích của hình nón?
- Định lý Pytago được áp dụng như thế nào trong bài toán hình nón?
- Bài 7 trang 134 SGK Toán 9 thường yêu cầu tính toán những đại lượng nào?
- Làm sao để vẽ hình nón chính xác?
- Có những dạng bài tập nào liên quan đến hình nón?
- Ứng dụng của hình nón trong thực tế là gì?
Khi cần hỗ trợ hãy liên hệ Email: Contact@badaovl.us, địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
