Bài 7 trang 49 SGK Toán Hình 12 là một bài tập quan trọng giúp học sinh làm quen với khái niệm mặt cầu và vị trí tương đối giữa mặt cầu với mặt phẳng. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết bài tập này mà còn là nền tảng vững chắc cho các bài toán phức tạp hơn trong chương trình hình học không gian lớp 12.
Tìm Hiểu Về Mặt Cầu Và Bài Toán 7 Trang 49
Bài 7 trang 49 yêu cầu chúng ta xác định vị trí tương đối giữa mặt cầu và mặt phẳng. Để giải quyết bài toán này, trước tiên cần hiểu rõ định nghĩa mặt cầu và phương trình mặt cầu. Mặt cầu là tập hợp tất cả các điểm trong không gian cách đều một điểm cố định (tâm) một khoảng cách không đổi (bán kính). Phương trình mặt cầu tâm I(a, b, c) và bán kính R có dạng (x-a)² + (y-b)² + (z-c)² = R². Vị trí tương đối giữa mặt cầu và mặt phẳng có 3 trường hợp: cắt nhau, tiếp xúc và không cắt nhau.
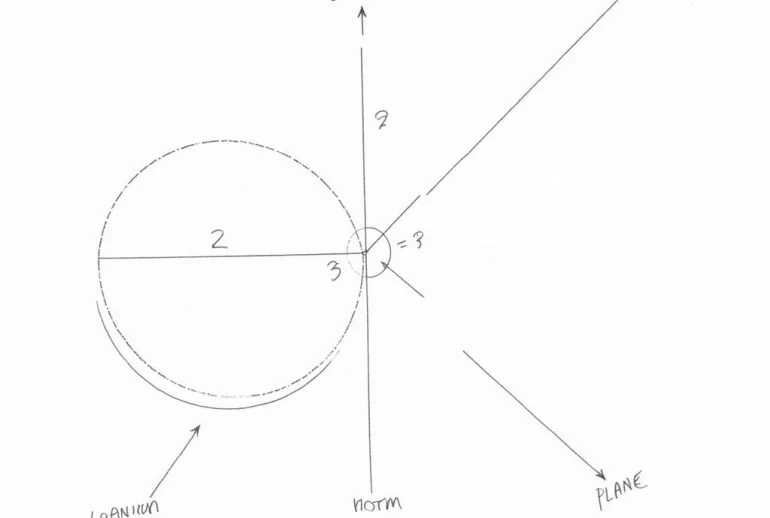
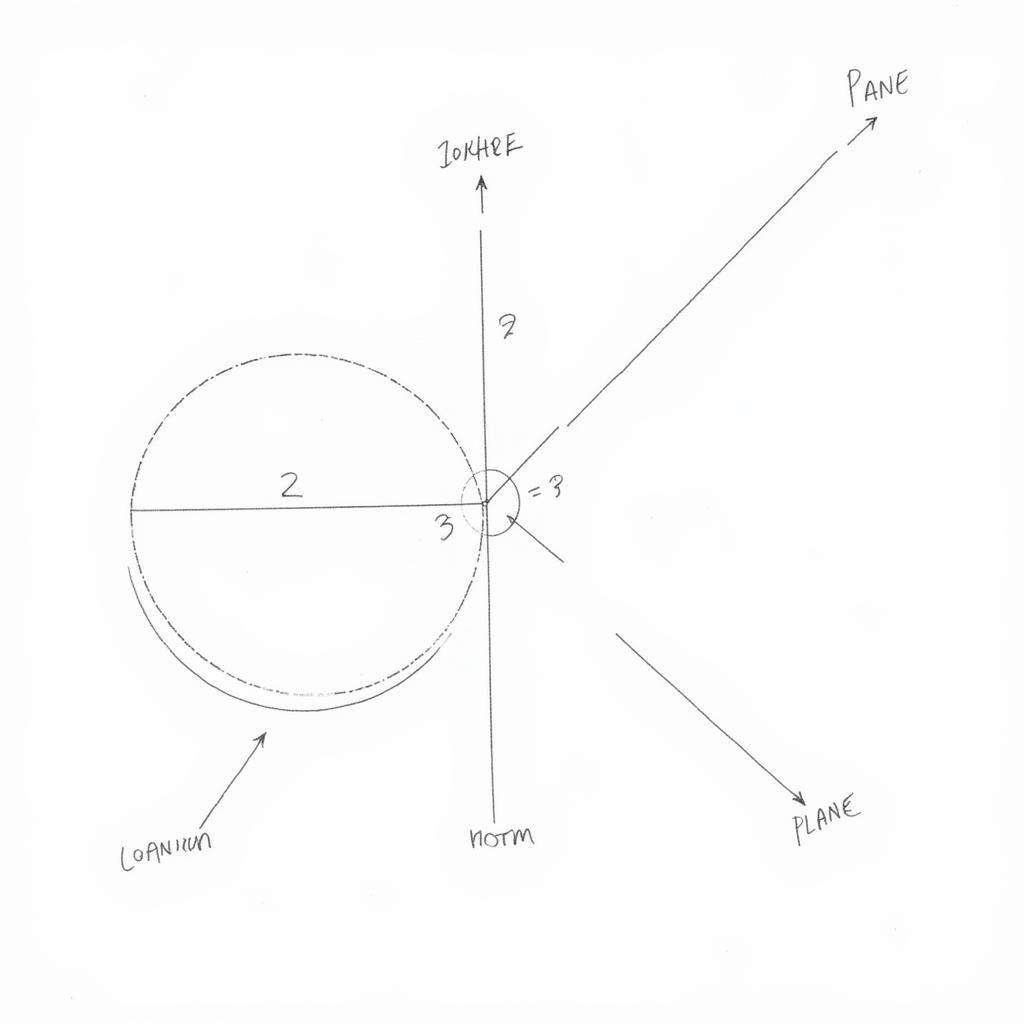Vị trí tương đối giữa mặt cầu và mặt phẳng
Để xác định vị trí tương đối, ta tính khoảng cách từ tâm mặt cầu đến mặt phẳng. Nếu khoảng cách này nhỏ hơn bán kính, mặt phẳng cắt mặt cầu. Nếu bằng bán kính, mặt phẳng tiếp xúc mặt cầu. Nếu lớn hơn bán kính, mặt phẳng không cắt mặt cầu.
Hướng Dẫn Giải Chi Tiết Bài 7 Trang 49 SGK Toán Hình 12
Đề bài thường cho phương trình mặt cầu và phương trình mặt phẳng. Bước đầu tiên là xác định tâm và bán kính của mặt cầu, sau đó tính khoảng cách từ tâm mặt cầu đến mặt phẳng. So sánh khoảng cách này với bán kính để kết luận về vị trí tương đối.
Ví dụ, cho mặt cầu (S): (x-1)² + (y+2)² + (z-3)² = 9 và mặt phẳng (P): 2x + y – 2z + 3 = 0. Tâm mặt cầu I(1, -2, 3) và bán kính R = 3. Khoảng cách từ I đến (P) là d = |2(1) + (-2) – 2(3) + 3|/√(2² + 1² + (-2)²) = |-3|/3 = 1. Vì d < R nên mặt phẳng (P) cắt mặt cầu (S).
Mẹo Giải Nhanh Bài Toán Vị Trí Tương Đối
Một số mẹo giúp bạn giải nhanh bài toán này là nhớ công thức tính khoảng cách và so sánh nhanh với bán kính. Ngoài ra, việc vẽ hình minh họa cũng giúp bạn hình dung rõ hơn về vị trí tương đối.
Ứng Dụng Của Mặt Cầu Trong Thực Tế
Mặt cầu có rất nhiều ứng dụng trong thực tế, từ thiết kế kiến trúc đến khoa học vũ trụ. Ví dụ, hình dạng của trái đất gần giống một mặt cầu.
Lời khuyên từ chuyên gia
Theo Tiến sĩ Nguyễn Văn A, chuyên gia toán học: “Việc nắm vững kiến thức về mặt cầu là rất quan trọng, không chỉ trong toán học mà còn trong nhiều lĩnh vực khác.”
giải bài 16 sgk toán 9 tập 1 trang 51
Câu hỏi thường gặp khi giải bài 7 trang 49
Làm thế nào để nhớ công thức tính khoảng cách?
cách giải bài tập các dạng con lac don
Kết Luận
Bài toán Giải Bài 7 Trang 49 Sgk Toán Hình 12 về mặt cầu không hề khó nếu bạn nắm vững kiến thức cơ bản và phương pháp giải. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về vấn đề này.
FAQ
- Làm sao để xác định tâm và bán kính của mặt cầu?
- Có bao nhiêu vị trí tương đối giữa mặt cầu và mặt phẳng?
- Khoảng cách từ tâm mặt cầu đến mặt phẳng được tính như thế nào?
- Làm sao để phân biệt ba trường hợp vị trí tương đối?
- Bài toán này có ứng dụng gì trong thực tế?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc xác định tâm và bán kính mặt cầu từ phương trình, cũng như tính toán khoảng cách.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về mặt cầu và các bài toán liên quan tại giải bài toán lớp 3 trang 4.
