Bạn đang gặp khó khăn với bài tập 6 trang 9 sách giáo khoa Toán 10? Đừng lo lắng! Bài viết này sẽ cung cấp lời giải chi tiết, dễ hiểu cho bài tập 6 sgk trang 9 toán 10, kèm theo những bài tập mở rộng giúp bạn nắm vững kiến thức.
Phần lớn học sinh lớp 10 đều cảm thấy bối rối khi bắt đầu làm quen với các khái niệm tập hợp trong chương trình Toán 10. Bài tập 6 trang 9 SGK Toán 10 là một ví dụ điển hình. Nắm vững bài tập này sẽ giúp các em có nền tảng vững chắc cho các bài toán tập hợp phức tạp hơn. Chúng ta sẽ cùng nhau phân tích đề bài, tìm ra lời giải và mở rộng kiến thức với các dạng bài tương tự.
Giải Chi Tiết Bài Tập 6 Trang 9 SGK Toán 10
Đề bài yêu cầu xác định các tập hợp sau và biểu diễn chúng trên trục số: A = {x ∈ ℝ | (2x – x^2)(2x^2 – 3x – 2) = 0} và B = {n ∈ ℕ* | 3 < n^2 < 30}. Để giải bài tập này, chúng ta cần giải quyết từng tập hợp riêng biệt.
Tìm Tập Hợp A
Đầu tiên, ta giải phương trình (2x – x^2)(2x^2 – 3x – 2) = 0. Phương trình này tương đương với 2x – x^2 = 0 hoặc 2x^2 – 3x – 2 = 0. Giải ra, ta được x = 0, x = 2, x = -1/2, x = 2. Vậy A = {-1/2, 0, 2}.
Tìm Tập Hợp B
Tiếp theo, ta xét bất đẳng thức 3 < n^2 < 30. Vì n ∈ ℕ* nên n là số nguyên dương. Bình phương các số nguyên dương và so sánh với 3 và 30, ta thấy n có thể nhận các giá trị 2, 3, 4, 5. Vậy B = {2, 3, 4, 5}.
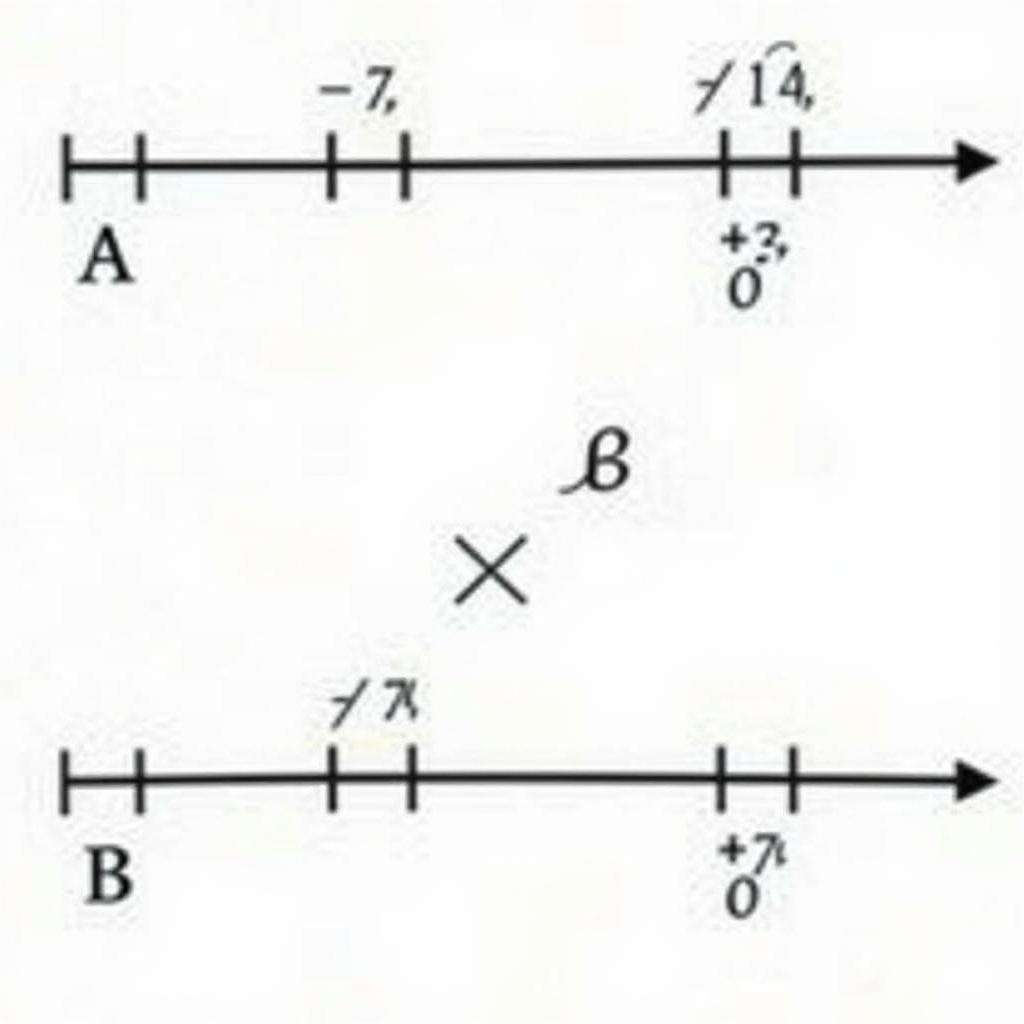Giải bài tập 6 sgk toán 10 trang 9 biểu diễn trên trục số
Biểu diễn A và B trên trục số khá đơn giản. Đối với tập A, ta đánh dấu các điểm -1/2, 0 và 2. Đối với tập B, ta đánh dấu các điểm 2, 3, 4 và 5.
Bài Tập Mở Rộng
Để củng cố kiến thức, hãy thử sức với một số bài tập mở rộng sau:
- Xác định tập hợp C = {x ∈ ℝ | x^3 – 3x^2 + 2x = 0} và biểu diễn trên trục số.
- Tìm tập hợp D = {n ∈ ℕ | n^2 – 5n + 6 < 0}.
- Cho E = {x ∈ ℝ | |x – 2| ≤ 1}. Biểu diễn E trên trục số.
Kết Luận
Bài viết đã hướng dẫn Giải Bài Tập 6 Sgk Trang 9 Toán 10 một cách chi tiết và dễ hiểu. Hy vọng qua bài viết này, bạn đã nắm vững kiến thức về tập hợp và cách biểu diễn chúng trên trục số. giải bài tập 5 sgk lopws7 trang 27
FAQ
-
Tập hợp là gì? Tập hợp là một khái niệm cơ bản trong toán học, dùng để chỉ một nhóm các đối tượng được xác định rõ ràng.
-
Làm thế nào để biểu diễn tập hợp trên trục số? Đối với tập hợp các số thực, ta biểu diễn bằng cách đánh dấu các điểm tương ứng trên trục số.
-
*ℕ là gì?* ℕ là tập hợp các số tự nhiên khác 0.
-
ℝ là gì? ℝ là tập hợp các số thực.
-
Tại sao cần học về tập hợp? Tập hợp là nền tảng cho nhiều khái niệm toán học khác.
các bài toán hình lớp 9 và cách giải
giải bài 61 sgk toán 9 tập 1 trang 166
Mô tả các tình huống thường gặp câu hỏi
Học sinh thường gặp khó khăn trong việc xác định điều kiện của biến và giải các phương trình, bất phương trình để tìm ra tập hợp. Việc biểu diễn tập hợp trên trục số cũng là một vấn đề cần được lưu ý.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tham khảo thêm giải bài 2 hoặc giải bài tập hóa hữu cơ đại học y dược trên website của chúng tôi.
