Giải bài tập chứng minh 3 điểm thẳng hàng lớp 7 là một trong những dạng bài toán hình học cơ bản nhưng quan trọng, giúp học sinh rèn luyện tư duy logic và khả năng vận dụng kiến thức. Bài viết này sẽ hướng dẫn chi tiết cách Giải Bài Tập Cm 3 điểm Thẳng Hàng Lớp 7, cung cấp các ví dụ minh họa và bài tập thực hành để bạn nắm vững kiến thức này.
Phương Pháp Chứng Minh 3 Điểm Thẳng Hàng Lớp 7
Có nhiều cách để chứng minh ba điểm thẳng hàng trong hình học lớp 7. Dưới đây là một số phương pháp phổ biến và dễ áp dụng:
- Sử dụng hai góc kề bù: Nếu tổng hai góc kề nhau bằng 180 độ, thì ba điểm tạo thành hai cạnh của hai góc đó thẳng hàng.
- Chứng minh tổng ba đoạn thẳng bằng nhau: Nếu AB + BC = AC, thì ba điểm A, B, C thẳng hàng. Đây là cách tiếp cận dựa trên tính chất cộng đoạn thẳng.
- Sử dụng tính chất đường trung trực: Nếu một điểm nằm trên đường trung trực của một đoạn thẳng, thì điểm đó cách đều hai đầu mút của đoạn thẳng.
- Dựa vào tia phân giác: Chứng minh hai tia là tia phân giác của hai góc kề bù.
Ví Dụ Giải Bài Tập CM 3 Điểm Thẳng Hàng Lớp 7
Để hiểu rõ hơn về cách áp dụng các phương pháp trên, chúng ta cùng xem xét một số ví dụ cụ thể:
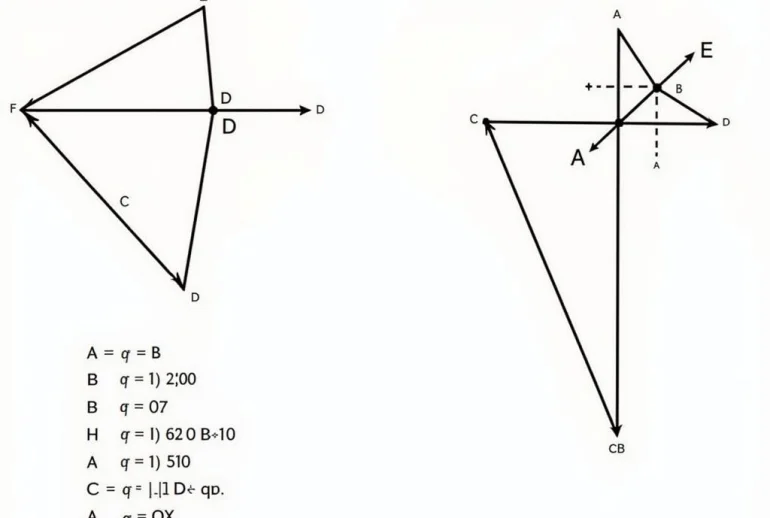
Ví dụ 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AC. Trên tia đối của tia AC lấy điểm E sao cho AE = AB. Chứng minh B, C, và trung điểm M của DE thẳng hàng.
Lời giải:
Gọi M là trung điểm của DE. Ta có DM = ME.
Xét tam giác ADB và tam giác AEC, ta có:
- AD = AC (giả thiết)
- AB = AE (giả thiết)
- góc BAD = góc CAE (hai góc đối đỉnh)
Vậy tam giác ADB bằng tam giác AEC (c.g.c).
Suy ra BD = CE.
Xét tam giác MBD và tam giác MCE, ta có:
- BD = CE (chứng minh trên)
- MD = ME (M là trung điểm DE)
- góc BDM = góc CEM (tam giác ADB bằng tam giác AEC)
Vậy tam giác MBD bằng tam giác MCE (c.g.c).
Suy ra góc BMD = góc CME. Mà góc BMD + góc CME + góc BMC = 180 độ (kề bù), nên 2*góc BMC = 180 độ. Vậy góc BMC = 90 độ, hay ba điểm B, C, M thẳng hàng.
Bài Tập Thực Hành Giải Bài Tập CM 3 Điểm Thẳng Hàng
Dưới đây là một số bài tập để bạn tự luyện tập:
Bài tập 1: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh rằng A, D, E thẳng hàng.
Bài tập 2: Cho góc xOy. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC và OB = OD. Chứng minh rằng AC // BD. (Gợi ý: Chứng minh trung điểm của AC và BD cùng nằm trên tia phân giác của góc xOy).
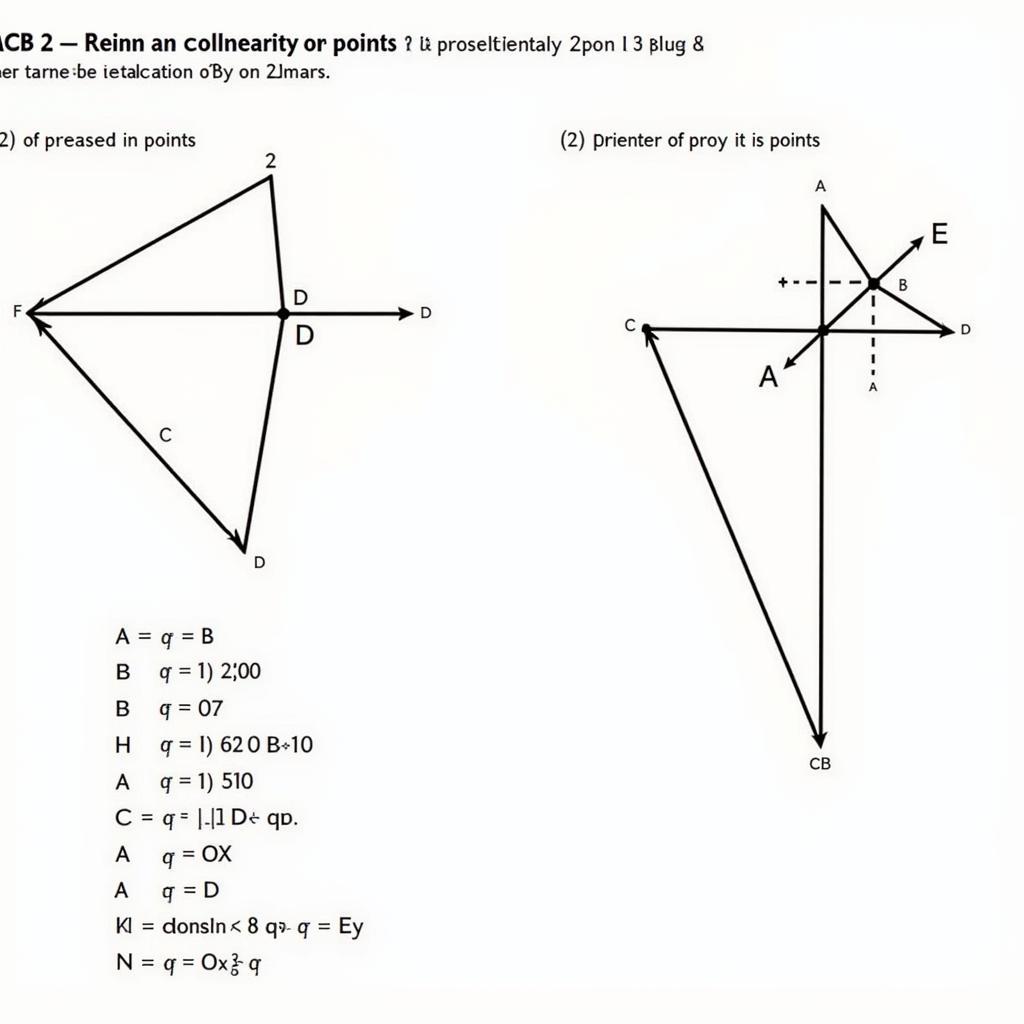Bài tập chứng minh ba điểm thẳng hàng
Kết Luận
Việc giải bài tập chứng minh 3 điểm thẳng hàng lớp 7 đòi hỏi sự kết hợp giữa kiến thức lý thuyết và khả năng tư duy logic. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để giải quyết dạng bài toán này một cách hiệu quả. Nắm vững các phương pháp chứng minh 3 điểm thẳng hàng sẽ giúp bạn tự tin hơn trong việc học tập môn hình học.
FAQ
-
Có những phương pháp nào để chứng minh 3 điểm thẳng hàng? Có nhiều phương pháp, bao gồm sử dụng hai góc kề bù, chứng minh tổng ba đoạn thẳng bằng nhau, sử dụng tính chất đường trung trực, và dựa vào tia phân giác.
-
Làm thế nào để nhận biết khi nào nên sử dụng phương pháp nào? Việc lựa chọn phương pháp phụ thuộc vào dữ kiện của bài toán. Cần phân tích đề bài để tìm ra cách tiếp cận phù hợp.
-
Bài toán chứng minh 3 điểm thẳng hàng thường xuất hiện trong những dạng bài nào? Dạng bài này thường xuất hiện trong các bài toán liên quan đến tam giác, đường trung trực, tia phân giác, v.v.
-
Tôi cần luyện tập thêm ở đâu để nâng cao kỹ năng giải bài tập này? Bạn có thể tìm thêm các bài tập trong sách giáo khoa, sách bài tập, hoặc các tài liệu tham khảo khác.
-
Làm sao để phân biệt giữa chứng minh ba điểm thẳng hàng và chứng minh hai đường thẳng song song? Chứng minh ba điểm thẳng hàng là chứng minh ba điểm nằm trên cùng một đường thẳng. Chứng minh hai đường thẳng song song là chứng minh hai đường thẳng không có điểm chung.
Bạn có thể tìm thấy thêm các bài viết liên quan đến hình học lớp 7 trên website của chúng tôi.
Khi cần hỗ trợ hãy liên hệ Email: Contact@badaovl.us, địa chỉ: Tòa nhà Etown Central, 11 Đoàn Văn Bơ, Quận 4, TP. Hồ Chí Minh, Việt Nam.. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
