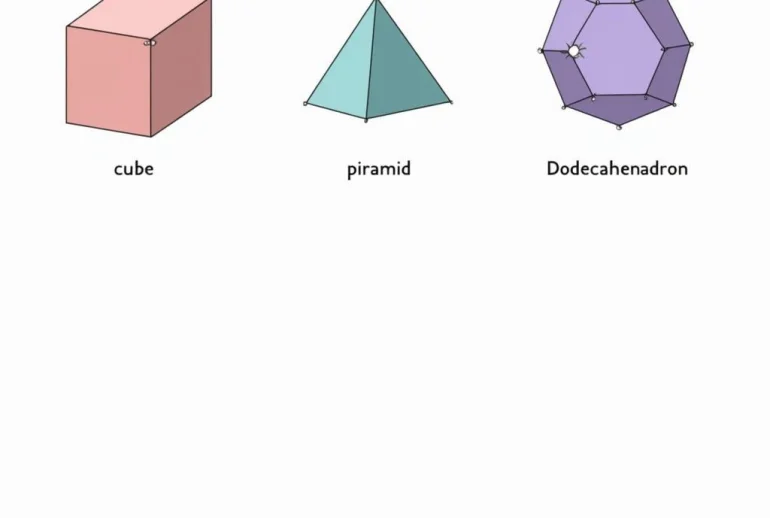
Khối đa diện là một phần quan trọng trong hình học không gian, việc nắm vững khái niệm này là nền tảng để giải quyết các bài tập liên quan. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện về khối đa diện, từ định nghĩa, các loại khối đa diện đến cách giải các bài tập từ cơ bản đến nâng cao.
Khái Niệm Cơ Bản Về Khối Đa Diện
Khối đa diện là hình được tạo bởi một số hữu hạn các đa giác phẳng thỏa mãn hai điều kiện:
- Hai đa giác bất kỳ hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
- Mỗi cạnh của một đa giác nào đó là cạnh chung của đúng hai đa giác.
Các đa giác tạo nên khối đa diện được gọi là các mặt, các cạnh chung của hai mặt được gọi là cạnh của khối đa diện, các đỉnh chung của các mặt là đỉnh của khối đa diện. Việc hiểu rõ định nghĩa này sẽ giúp bạn phân biệt khối đa diện với các hình không gian khác.
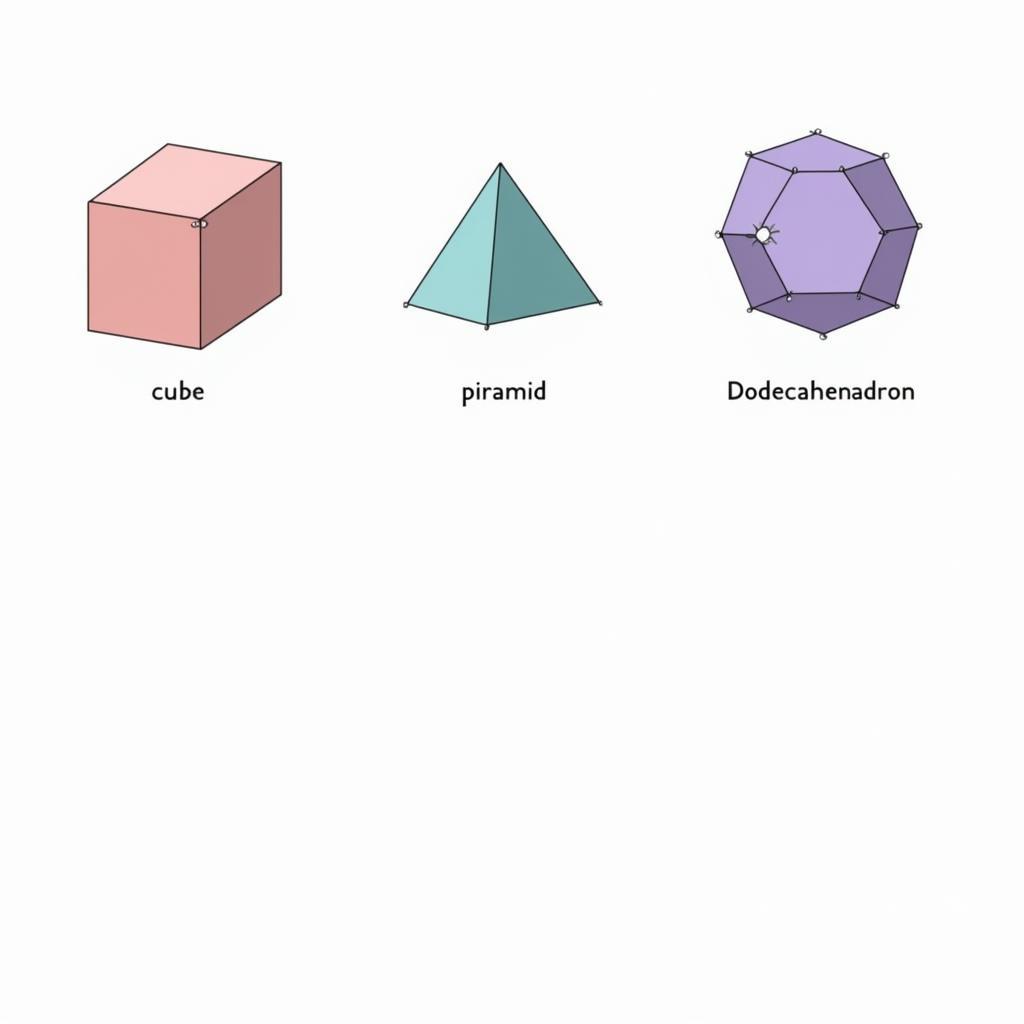Khối Đa Diện Các Loại
Phân Loại Khối Đa Diện
Khối đa diện được phân loại dựa trên số mặt của chúng. Một số loại khối đa diện thường gặp bao gồm:
- Khối đa diện lồi: Là khối đa diện luôn nằm về một phía của mặt phẳng chứa bất kỳ mặt nào của nó. Đây là loại khối đa diện thường gặp nhất trong các bài tập.
- Khối đa diện đều: Là khối đa diện lồi có tất cả các mặt là các đa giác đều bằng nhau và các góc đa diện bằng nhau. Ví dụ như khối lập phương, khối tứ diện đều.
- Hình lăng trụ: Là khối đa diện có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song, và các mặt bên là hình bình hành.
Việc phân loại khối đa diện giúp chúng ta dễ dàng nhận diện và áp dụng các công thức tính toán phù hợp. giải bài tập hóa học 8 bài 4 trang 11 cung cấp kiến thức nền tảng để giải quyết các vấn đề liên quan.
Giải Bài Tập Khái Niệm Về Khối Đa Diện
Để giải quyết các bài tập liên quan đến khối đa diện, bạn cần nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của các loại khối đa diện khác nhau. Bên cạnh đó, việc vẽ hình và phân tích đề bài cũng rất quan trọng. Dưới đây là một số ví dụ minh họa:
Ví dụ 1: Cho hình lập phương có cạnh bằng a. Tính diện tích toàn phần và thể tích của hình lập phương.
Giải:
- Diện tích toàn phần: 6a²
- Thể tích: a³
Ví dụ 2: Cho hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h. Tính diện tích xung quanh và thể tích của hình chóp.
Giải:
- Diện tích xung quanh: 2a√(h² + (a/2)²)
- Thể tích: (1/3)a²h
Những ví dụ trên chỉ là một phần nhỏ trong vô số các bài tập về khối đa diện. bài tập giải tích 12 chương 1 trần sĩ tùng cung cấp thêm các bài tập nâng cao giúp bạn rèn luyện kỹ năng giải toán.
Kết Luận
Hiểu rõ khái niệm về khối đa diện là bước đầu tiên và quan trọng để giải quyết các bài tập hình học không gian. Bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hướng dẫn giải bài tập liên quan đến “giải bài tập khái niệm về khối đa diện”. Hy vọng bài viết này sẽ hữu ích cho bạn. giải bài tập hình học 12 ôn tập chương 2 sẽ giúp bạn củng cố kiến thức về hình học không gian.
FAQ
- Khối đa diện là gì?
- Phân loại khối đa diện như thế nào?
- Công thức tính diện tích toàn phần của hình lập phương là gì?
- Làm thế nào để tính thể tích của hình chóp?
- Khối đa diện lồi khác gì so với khối đa diện đều?
- Cho ví dụ về một số khối đa diện thường gặp?
- cách giải bài toán hiệu suất tạo thành có liên quan gì đến khối đa diện không?
Mô tả các tình huống thường gặp câu hỏi
Học sinh thường gặp khó khăn trong việc hình dung khối đa diện trong không gian và áp dụng công thức tính toán. Việc phân biệt các loại khối đa diện cũng là một thách thức.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các bài tập hình học không gian khác tại giải bài tập hóa sgk 11.
