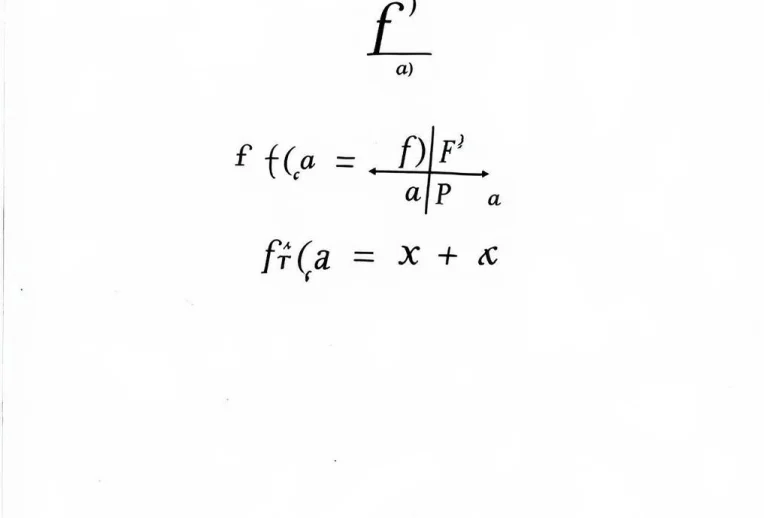Giải Bài Tập Khai Triển Taylor Maclaurin là một kỹ năng quan trọng trong giải tích. Bài viết này sẽ hướng dẫn bạn cách áp dụng khai triển Taylor và Maclaurin để giải quyết các bài toán từ cơ bản đến nâng cao, cùng với những ví dụ minh họa cụ thể và các mẹo hữu ích.
Tìm Hiểu Về Khai Triển Taylor và Maclaurin
Khai triển Taylor cho phép chúng ta xấp xỉ một hàm số khả vi bằng một đa thức tại một điểm cụ thể. Khai triển Maclaurin là một trường hợp đặc biệt của khai triển Taylor, khi điểm đó là 0. Chúng ta có thể sử dụng khai triển này để tính toán giá trị hàm số, giải phương trình, và nhiều ứng dụng khác trong toán học và vật lý.
Công Thức Khai Triển Taylor
Công thức chung cho khai triển Taylor của hàm f(x) tại điểm x = a là:
f(x) = f(a) + f'(a)(x-a) + f”(a)(x-a)²/2! + f”'(a)(x-a)³/3! + …
 Công Thức Khai Triển Taylor
Công Thức Khai Triển Taylor
Công Thức Khai Triển Maclaurin
Khi a = 0, ta có khai triển Maclaurin:
f(x) = f(0) + f'(0)x + f”(0)x²/2! + f”'(0)x³/3! + …
Khi Nào Nên Sử Dụng Khai Triển Taylor Maclaurin?
Khai triển Taylor Maclaurin hữu ích khi ta cần xấp xỉ giá trị của một hàm số phức tạp tại một điểm cụ thể, đặc biệt khi việc tính toán trực tiếp gặp khó khăn. Nó cũng được dùng để giải các phương trình vi phân và tích phân.
Ví Dụ Giải Bài Tập Khai Triển Taylor Maclaurin
Hãy cùng xem xét một số ví dụ để hiểu rõ hơn về cách áp dụng khai triển Taylor Maclaurin.
Ví dụ 1: Khai triển Maclaurin của hàm e^x
Ta có f(x) = e^x. Các đạo hàm của f(x) đều là e^x. Tại x = 0, f(0) = f'(0) = f”(0) = … = 1. Do đó, khai triển Maclaurin của e^x là:
e^x = 1 + x + x²/2! + x³/3! + …
Ví dụ 2: Khai triển Taylor của hàm sin(x) tại x = π/2
Ta có f(x) = sin(x). f(π/2) = 1, f'(π/2) = 0, f”(π/2) = -1, f”'(π/2) = 0, … . Khai triển Taylor của sin(x) tại x = π/2 là:
sin(x) = 1 – (x-π/2)²/2! + (x-π/2)⁴/4! – …
Mẹo Giải Bài Tập Khai Triển Taylor Maclaurin
- Nắm vững công thức: Việc hiểu rõ công thức khai triển là bước đầu tiên và quan trọng nhất.
- Tính đạo hàm chính xác: Sai lầm trong tính đạo hàm sẽ dẫn đến kết quả sai.
- Xác định điểm khai triển: Chọn điểm khai triển phù hợp để việc tính toán trở nên đơn giản hơn.
Giả sử bạn là một học sinh đang gặp khó khăn với bài tập khai triển Taylor. Bạn có thể tìm thấy lời giải chi tiết và hướng dẫn học tập tại bài tập về khai triển maclaurin có lời giải.
Kết luận
Giải bài tập khai triển Taylor Maclaurin đòi hỏi sự chính xác và kiên nhẫn. Bằng cách nắm vững công thức, thực hành nhiều bài tập, và áp dụng các mẹo hữu ích, bạn sẽ có thể giải quyết các bài toán một cách hiệu quả. Hi vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về giải bài tập khai triển Taylor Maclaurin.
FAQ
- Khai triển Taylor và Maclaurin khác nhau như thế nào?
- Làm thế nào để xác định bậc của khai triển Taylor?
- Ứng dụng của khai triển Taylor Maclaurin trong thực tế là gì?
- Khi nào thì khai triển Taylor Maclaurin hội tụ?
- Có những phương pháp nào để kiểm tra kết quả khai triển?
- Tôi có thể tìm thấy thêm bài tập về khai triển Taylor Maclaurin ở đâu?
- Làm thế nào để tính đạo hàm của hàm phức tạp?
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn khi tính đạo hàm cấp cao, xác định điểm khai triển phù hợp, và áp dụng công thức khai triển cho các hàm số phức tạp.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như giới hạn, đạo hàm, tích phân, và các bài tập về khai triển maclaurin có lời giải.