Giải Bài Toán Cân Bằng Cơ Hệ là một kỹ năng quan trọng trong vật lý, đặc biệt là trong chương trình học lớp 10. Bài viết này sẽ cung cấp cho bạn những phương pháp và ví dụ minh họa chi tiết để giải quyết các bài toán cân bằng cơ hệ từ cơ bản đến nâng cao.
Để giải quyết bài toán cân bằng cơ hệ, trước hết ta cần hiểu rõ khái niệm cân bằng. Một vật được coi là cân bằng khi nó đứng yên hoặc chuyển động thẳng đều. Điều này có nghĩa là tổng các lực tác dụng lên vật bằng không và tổng các mômen lực tác dụng lên vật cũng bằng không.
Phương Pháp Giải Bài Toán Cân Bằng Cơ Hệ
Để giải bài toán cân bằng cơ hệ, ta có thể áp dụng các bước sau:
- Xác định tất cả các lực tác dụng lên vật.
- Chọn một điểm làm điểm tựa.
- Viết phương trình cân bằng lực theo các trục x, y.
- Viết phương trình cân bằng mômen lực.
- Giải hệ phương trình để tìm các đại lượng chưa biết.
Ví Dụ Minh Họa Giải Bài Toán Cân Bằng Cơ Hệ
Xét một thanh đồng chất, chiều dài l, khối lượng m, được treo bằng hai sợi dây nhẹ, không dãn tại hai đầu. Tìm lực căng của mỗi dây.
Giải:
- Các lực tác dụng lên thanh gồm trọng lực P = mg và lực căng T1, T2 của hai dây.
- Chọn điểm treo của một dây làm điểm tựa.
- Phương trình cân bằng lực: T1 + T2 = P.
- Phương trình cân bằng mômen lực: T2 l = P l/2.
- Giải hệ phương trình ta được T1 = T2 = P/2 = mg/2.
“Trong vật lý, việc nắm vững nguyên tắc cân bằng lực và mômen lực là chìa khóa để giải quyết các bài toán cân bằng cơ hệ,” – PGS.TS Nguyễn Văn An, chuyên gia vật lý tại Đại học Khoa học Tự nhiên, chia sẻ.
Giải Bài Toán Cân Bằng Cơ Hệ Với Lực Ma Sát
Khi có lực ma sát, bài toán cân bằng cơ hệ sẽ phức tạp hơn. Ta cần xem xét cả lực ma sát tĩnh và lực ma sát động.
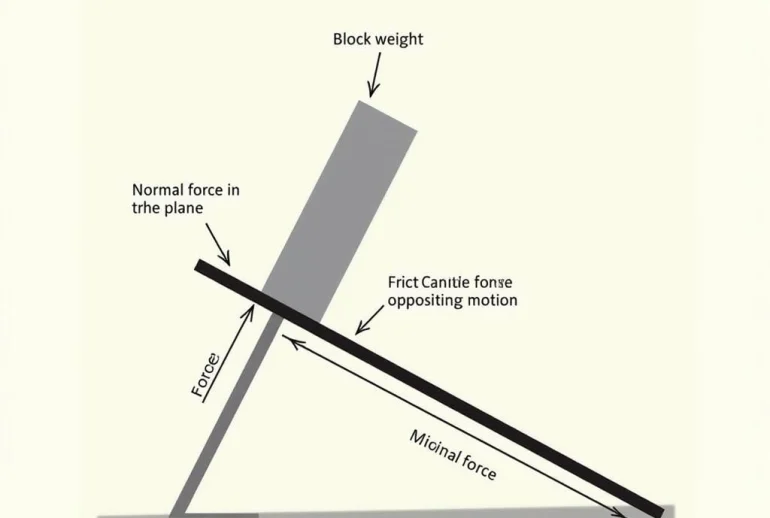
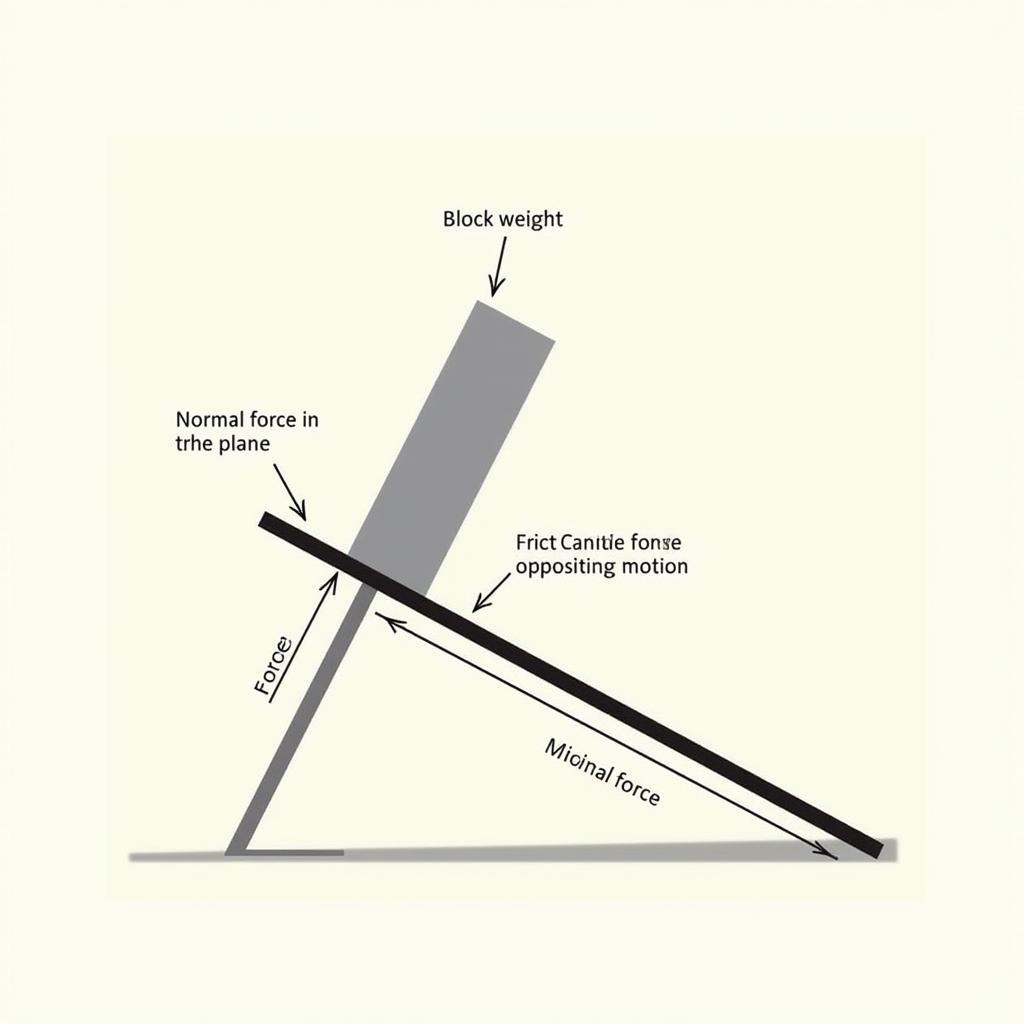Giải bài toán cân bằng cơ hệ với lực ma sát
Ví dụ: Một vật khối lượng m đặt trên mặt phẳng nghiêng góc α. Hệ số ma sát giữa vật và mặt phẳng là μ. Tìm điều kiện để vật cân bằng.
Giải:
Phân tích lực tác dụng lên vật, ta có trọng lực P, phản lực N và lực ma sát Fms. Điều kiện cân bằng là:
- Theo phương vuông góc với mặt phẳng nghiêng: N = Pcosα.
- Theo phương song song với mặt phẳng nghiêng: Fms = Psinα.
- Điều kiện để vật cân bằng là Fms ≤ μN, tức là Psinα ≤ μPcosα, hay tanα ≤ μ.
“Việc giải bài toán cân bằng cơ hệ có ma sát đòi hỏi sự tỉ mỉ trong việc phân tích lực và áp dụng đúng công thức,” – ThS. Lê Thị Mai, giảng viên vật lý tại trường THPT chuyên Hà Nội – Amsterdam, nhận định.
Kết luận
Giải bài toán cân bằng cơ hệ là một phần quan trọng trong chương trình vật lý. Hiểu rõ các nguyên tắc và phương pháp giải sẽ giúp bạn giải quyết các bài toán này một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về giải bài toán cân bằng cơ hệ.
Bạn có thể tìm hiểu thêm về giải bài 12 sgk toán 9 tập 1 trang 11 và giải toán 9 bài 43 trang 27 trên BaDaoVl.
FAQ
- Khi nào một vật được coi là cân bằng?
- Các bước để giải bài toán cân bằng cơ hệ là gì?
- Lực ma sát ảnh hưởng như thế nào đến bài toán cân bằng cơ hệ?
- Làm thế nào để xác định điểm tựa trong bài toán cân bằng cơ hệ?
- Có những loại cân bằng cơ hệ nào?
- Làm sao để phân biệt bài toán cân bằng tĩnh và cân bằng động?
- Ứng dụng của bài toán cân bằng cơ hệ trong thực tế là gì?
Xem thêm bài tập toán lớp 7 có lời giải tập 2 và bài tập toán 11 nâng cao có lời giải để củng cố kiến thức toán học.
Mô tả các tình huống thường gặp câu hỏi.
Học sinh thường gặp khó khăn trong việc xác định các lực tác dụng lên vật và chọn điểm tựa phù hợp. Việc phân tích lực ma sát cũng là một thách thức đối với nhiều học sinh.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các cách giải bài toán lớp 5 trên BaDaoVl.
